Câu hỏi:

19/08/2025 1,131

Trên cạnh BC của hình vuông ABCD cạnh 6, lấy điểm E sao cho $C F = 3$ . Trên tia đối của tia CD lấy điểm F sao cho . Gọi M là giao điểm của AE và BF. Tính góc AMC.

Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 1 và 2: Tổng hợp định lí ta-lét, tam giác đồng dạng và các bài toán liên quan có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

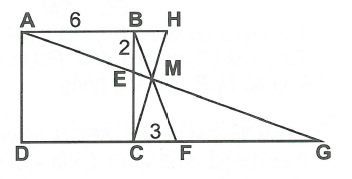
Media VietJack

Gọi H là giao điểm của CM và AB, G là giao điểm của AM và DF.

Vì $A B / / C G$ nên $\frac{A B}{C G} = \frac{B E}{E C} = \frac{B E}{B C - B E} = \frac{2}{6 - 2} = \frac{1}{2}$ (hệ quả định lý Ta-lét)

$\Rightarrow C G = 2 A B = 2.6 = 12 \Rightarrow F G = C G - C F = 12 - 3 = 9$

Vì $A H / / C G$ nên $\frac{B H}{A B} = \frac{C F}{F G}$

$\Rightarrow \frac{B H}{6} = \frac{3}{9} \Rightarrow B H = 6. \frac{3}{9} = 2 \Rightarrow B H = B E$

Xét $Δ B A E$ và $Δ B C H$ có:

$\{\begin{cases} B E = B H (theo treân) \\ \hat{A B E} = \hat{C B H} = 90 ° \\ A B = B C (tính chát hình vuong) \end{cases}$

$\Rightarrow Δ B A E = Δ B C H (c . g . c) \Rightarrow \hat{B E A} = \hat{B H C} \Rightarrow \hat{A M C} = \hat{M A H} + \hat{A H M} = \hat{M A H} + \hat{A E B} = 90 °$

Vậy $\hat{A M C} = 90 °$ .

Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC, $P Q / / B C$ với P, Q là các điểm tương ứng thuộc AB, AC. Đường thẳng PC và QB cắt nhau tại G. Đường thẳng đi qua G và song song với BC cắt AB tại E và AC tại F. Biết $P Q = a, F E = b$ . Tính độ dài của BC.

Xem đáp án

Lời giải

Định hướng

Sau khi vẽ hình ta thấy hình thang PQCB có đủ các điều kiện của Ví dụ 2 - dạng 1 - chủ đề 1. Do đó ta có thể sử dụng kết quả của Ví dụ 2 để giải quyết bài toán.

Lời giải

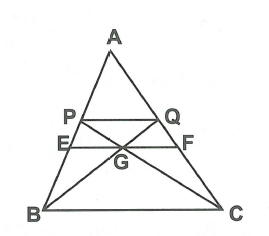
Media VietJack

Đặt $B C = x$ .

Áp dụng kết quả của Ví dụ 2 - dạng 1 - chủ đề 1 ta có:

$\frac{1}{G E} = \frac{1}{G F} = \frac{1}{a} + \frac{1}{x} \Rightarrow G E = G F = \frac{a x}{a + x}$

$\Rightarrow G E + G F = 2 \frac{a x}{a + x} \Leftrightarrow E F = \frac{2 a x}{a + x} \Leftrightarrow b = \frac{2 a x}{a + x}$

$\Leftrightarrow a b + b x - 2 a x = 0 \Leftrightarrow x = \frac{a b}{2 a - b}$

Vậy $B C = \frac{a b}{2 a - b}$ .

Câu 2

Cho hình thoi BEDF nội tiếp tam giác ABC (E thuộc AB, D thuộc AC, F thuộc BC).

Chứng minh $B D < \frac{2 a c}{a + c}$ với AB= c, BC=a.

Xem đáp án

Lời giải

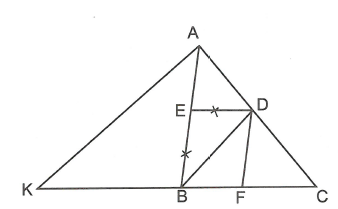
Media VietJack

Trên tia đối của tia BC lấy điểm K sao cho $B K = B A$ .

Ta có tam giác ABK cân tại B nên $\hat{B K A} = \hat{B A K} = \frac{1}{2} \hat{A B C}$ (tính chất góc ngoài tam giác).

Mà $\hat{E B D} = \hat{D B F} = \frac{1}{2} \hat{A B C} \Rightarrow \hat{A K B} = \hat{D B F} \Rightarrow B D / / A K \Rightarrow \frac{B D}{A K} = \frac{C B}{C K}$ (hệ quả định lý Ta-lét)

$\Rightarrow \frac{B D}{A K} = \frac{C B}{B C + B K} = \frac{a}{a + c}$ (1)

Trong tam giác ABK có:

$A K < A B + B K = c + c = 2 c$ (định lý về độ dài cạnh trong tam giác) (2).

Từ (1) và (2) có: $B D < \frac{a}{a + c} .2 c = \frac{2 a c}{a + c}$

Vậy $B D < \frac{2 a c}{a + c}$ .

Câu 3

Cho hình thoi BEDF nội tiếp tam giác ABC (E thuộc AB, D thuộc AC, F thuộc BC).

Tính độ dài AB, BC, biết AD=m, DC=n, DE=d.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình thoi BEDF nội tiếp tam giác ABC (E thuộc AB, D thuộc AC, F thuộc BC).

Tính cạnh hình thoi biết AB= c, BC=a.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Trên cạnh BC của hình vuông ABCD cạnh 6, lấy điểm E sao cho $C F = 3$ . Trên tia đối của tia CD lấy điểm F sao cho . Gọi M là giao điểm của AE và BF. Tính góc AMC.

Cho tam giác ABC, $P Q / / B C$ với P, Q là các điểm tương ứng thuộc AB, AC. Đường thẳng PC và QB cắt nhau tại G. Đường thẳng đi qua G và song song với BC cắt AB tại E và AC tại F. Biết $P Q = a, F E = b$ . Tính độ dài của BC.

Cho hình thoi BEDF nội tiếp tam giác ABC (E thuộc AB, D thuộc AC, F thuộc BC).

Chứng minh $B D < \frac{2 a c}{a + c}$ với AB= c, BC=a.

Cho hình thoi BEDF nội tiếp tam giác ABC (E thuộc AB, D thuộc AC, F thuộc BC).

Tính độ dài AB, BC, biết AD=m, DC=n, DE=d.

Cho hình thoi BEDF nội tiếp tam giác ABC (E thuộc AB, D thuộc AC, F thuộc BC).

Tính cạnh hình thoi biết AB= c, BC=a.