Cho tứ giác ABCD, vẽ các đường thẳng , song song với AC; cắt AD, DC theo thứ tự tại E và F; cắt AB, BC theo thứ tự tại G và H (G, H khác E, F). Chứng minh rằng EG, DB, HF đồng quy.
Cho tứ giác ABCD, vẽ các đường thẳng , song song với AC; cắt AD, DC theo thứ tự tại E và F; cắt AB, BC theo thứ tự tại G và H (G, H khác E, F). Chứng minh rằng EG, DB, HF đồng quy.
Quảng cáo
Trả lời:
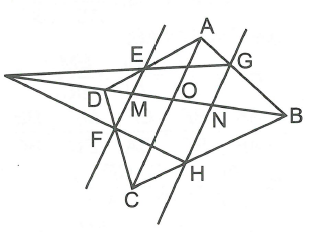
Gọi M, O, N lần lượt là giao điểm của EF, AC, GH với BD.
Vì nên (hệ quả định lý Ta-lét) (1).
Vì nên (hệ quả định lý Ta-lét) (2).
Từ (1) và (2) ta có: (*)
Tương tự có: (**)
Từ (*) và (**) có mà suy ra GE, BD, HF đồng quy. Vậy EG, DB, HF đồng quy.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
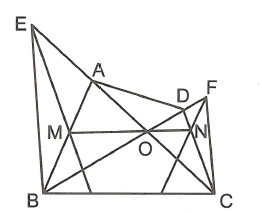
Vì nên (định lý Ta-lét) (1)
Vì nên (định lý Ta-lét) (2)
Từ (1) và (2) ta có (định lý Ta-lét đảo).
Vậy .
Lời giải
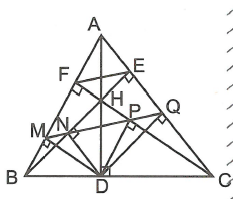
Vì (cùng vuông góc với AC) nên (định lý Ta-lét) (1).
Vì (cùng vuông góc với AB) nên (định lý Ta-lét) (2).
Từ (1) và (2) ta có (định lý Ta-lét đảo) (*).
Tương tự có (**)
Từ (*) và (**) có MN, MQ, PQ trùng nhau hay M, N, P, Q thẳng hàng. Vậy M, N, P, Q thẳng hàng