Cho hình thang ABCD , AD cắt BC tại I, AC cắt BD tại O. M, N lần lượt là trung điểm của AB, DC. Chứng minh rằng I, M, O, N thẳng hàng.
Cho hình thang ABCD , AD cắt BC tại I, AC cắt BD tại O. M, N lần lượt là trung điểm của AB, DC. Chứng minh rằng I, M, O, N thẳng hàng.
Quảng cáo
Trả lời:
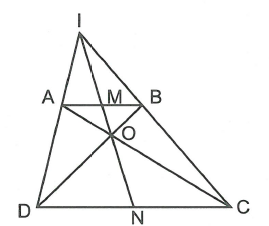
Vì M là trung điểm AB, N là trung điểm CD nên
Mà nên AC, MN, BD đồng quy hay O thuộc MN (1 ).
Lại có:
mà nên AD, MN, BC đồng quy hay I thuộc MN (2).
Từ (1 ) và (2) suy ra I, M, O, N thẳng hàng.
Nhận xét:
- Đây là bài toán đơn giản tuy nhiên được sử dụng rất nhiều với tên gọi Bổ đề hình thang: "Trong hình thang có hai cạnh đáy không bằng nhau, đường thẳng đi qua giao điểm của các đường thẳng chứa hai cạnh bên thì đi qua trung điểm của hai đáy"
- Ngược lại: Trong hình thang có hai cạnh đáy không bằng nhau, giao điểm của hai cạnh bên, giao điểm của hai đường chéo và trung điểm của hai đáy là các điểm thẳng hàng".
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
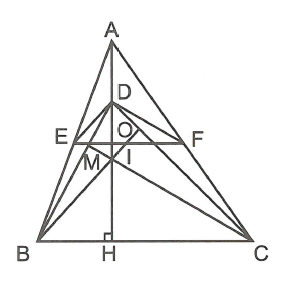
Kẻ
Gọi giao điểm của BO và CM là I.
Theo cách dựng suy ra D là trực tâm của tam giác BIC, suy ra thẳng hàng
(định lí Ta-lét).
Mặt khác (cùng vuông góc với BD)
nên (định lí Ta-lét đảo).
Vậy .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.