Câu hỏi:

30/10/2023 1,458

Cho tam giác ABC vuông cân tại A và tam giác MNP có MN = MP = 4 cm và NP = \(4\sqrt 2 \) cm. Chứng minh rằng ∆ABC ᔕ ∆MNP.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 8 KNTT Bài 36. Các trường hợp đồng dạng của hai tam giác vuông có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

Tam giác ABC vuông cân tại A nên \(\widehat B = 45^\circ \).

Vì MN² + MP² = NP² (do 4² + 4² = \({\left( {4\sqrt 2 } \right)^2}\))

Nên tam giác MNP vuông tại M (theo định lí Pythagore đảo).

Mà MN = MP = 4 cm nên tam giác MNP vuông cân tại M.

Do đó, \(\widehat N = 45^\circ \).

Xét tam giác ABC vuông ở A và tam giác MNP vuông ở M có:

\(\widehat B = \widehat N = 45^\circ \)

Do đó, ∆ABC ᔕ ∆MNP (hai góc nhọn bằng nhau).

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng:

a) HA . HD = HB . HE = HC . HF;

b) ∆AFC ᔕ ∆AEB và AF . AB = AE . AC;

c) ∆BDF ᔕ ∆EDC và DA là tia phân giác của góc EDF.

Xem đáp án

Lời giải

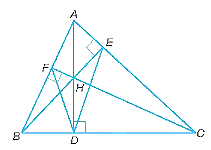
Media VietJack

Vì AD, BE, CF là các đường cao của tam giác ABC nên AD vuông góc với BC, BE vuông góc với AC, CF vuông góc với AB.

Tam giác AHE vuông ở H và tam giác BHD vuông ở D có:

\(\widehat {AHE} = \widehat {BHD}\) (hai góc đối đỉnh)

Do đó, ∆AHE ᔕ ∆BHD (góc nhọn).

Suy ra \(\frac{{AH}}{{BH}} = \frac{{HE}}{{HD}}\) nên HA . HD = HB . HE (1).

Tam giác HBF vuông ở F và tam giác HCE vuông ở E có:

\(\widehat {BHF} = \widehat {EHC}\) (hai góc đối đỉnh)

Do đó, ∆HBF ᔕ ∆HCE (góc nhọn).

Suy ra \(\frac{{HB}}{{HC}} = \frac{{HF}}{{HE}}\) nên HB . HE = HC . HF (2).

Từ (1) và (2) ta có: HA . HD = HB . HE = HC . HF.

Tam giác AFC vuông ở F và tam giác AEB vuông ở E có:

\(\widehat {BAC}\) chung.

Do đó, ∆AFC ᔕ ∆AEB (góc nhọn)

Suy ra \(\frac{{AF}}{{AE}} = \frac{{AC}}{{AB}}\) nên AF . AB = AE . AC.

Vì HA . HD = HB . HE nên \(\frac{{HA}}{{HE}} = \frac{{HB}}{{HD}}\)

Tam giác HAB và tam giác HED có:

\(\frac{{HA}}{{HE}} = \frac{{HB}}{{HD}}\) (cmt)

\(\widehat {AHB} = \widehat {EHD}\) (hai góc đối đỉnh)

Do đó, ∆AHB ᔕ ∆EHD (c.g.c).

Suy ra \(\widehat {HAB} = \widehat {HED}\).

Mà \(\widehat {HAB} + \widehat {FBD} = \widehat {HED} + \widehat {DEC}\) (= \(90^\circ \)).

Do đó, \(\widehat {FBD} = \widehat {DEC}\).

Chứng minh tương tự ta có: \(\widehat {BFD} = \widehat {ECD}\).

Tam giác BDF và tam giác EDC có:

\(\widehat {FBD} = \widehat {DEC}\) (cmt)

\(\widehat {BFD} = \widehat {ECD}\) (cmt)

Do đó, ∆BDF ᔕ ∆EDC (g.g).

Suy ra: \(\widehat {BDF} = \widehat {EDC}\).

Mà \[\widehat {BDF} + \widehat {FDH} = \widehat {EDC} + \widehat {HDE}\left( { = 90^\circ } \right)\].

Do đó, \(\widehat {FDH} = \widehat {HDE}\) hay \(\widehat {FDA} = \widehat {ADE}\).

Vậy DA là tia phân giác của góc EDF.

Câu 2

Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8 cm, hãy tính độ dài các đoạn thẳng BC, AH, BH, CH.

Xem đáp án

Lời giải

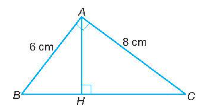
Media VietJack

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 6² + 8² = 100

Nên BC = 10 cm.

Vì AH là đường cao trong tam giác ABC nên AH vuông góc với BC.

Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:

\(\widehat C\) chung

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra \(\frac{{AC}}{{HC}} = \frac{{BC}}{{AC}}\) nên CH = \(\frac{{C{A^2}}}{{CB}} = \frac{{{8^2}}}{{10}} = \frac{{32}}{5} = 6,4\) (cm).

Do đó, BH = BC – CH = 10 – 6,4 = 3,6 (cm).

Vì ∆ABC ᔕ ∆HAC (cmt) nên \(\frac{{AB}}{{HA}} = \frac{{BC}}{{AC}}\).

Do đó, AH = \(\frac{{AB \cdot AC}}{{BC}} = \frac{{6 \cdot 8}}{{10}} = 4,8\) (cm).

Câu 3