Giải SBT Toán 8 KNTT Bài 36. Các trường hợp đồng dạng của hai tam giác vuông có đáp án
44 người thi tuần này 4.6 776 lượt thi 12 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Lời giải
Các điều kiện (1), (3), (4), (6) kéo theo hai tam giác vuông đồng dạng.
Giải thích: Các điều kiện (1), (3), (6) là theo các trường hợp bằng nhau của hai tam giác vuông. Điều kiện (4) suy ra một góc nhọn của tam giác này bằng một góc nhọn của tam giác kia (do cùng có tổng với góc nhọn còn lại bằng 90°), vậy quay trở về giống với điều kiện (1).
Lời giải
Lời giải
Tam giác ABC vuông cân tại A nên \(\widehat B = 45^\circ \).
Vì MN2 + MP2 = NP2 (do 42 + 42 = \({\left( {4\sqrt 2 } \right)^2}\))
Nên tam giác MNP vuông tại M (theo định lí Pythagore đảo).
Mà MN = MP = 4 cm nên tam giác MNP vuông cân tại M.
Do đó, \(\widehat N = 45^\circ \).
Xét tam giác ABC vuông ở A và tam giác MNP vuông ở M có:
\(\widehat B = \widehat N = 45^\circ \)
Do đó, ∆ABC ᔕ ∆MNP (hai góc nhọn bằng nhau).
Lời giải
Lời giải
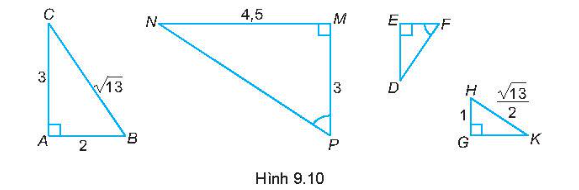
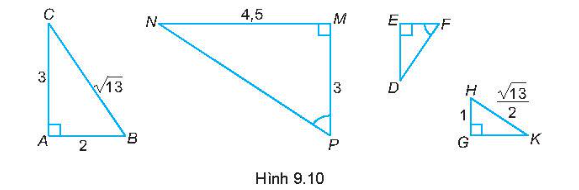
+) Tam giác ABC vuông ở A và tam giác MPN vuông ở M có:
\(\frac{{AB}}{{MP}} = \frac{{AC}}{{NM}}\) \(\left( {\frac{2}{3} = \frac{3}{{4,5}}} \right)\)
Do đó, ∆ABC ᔕ ∆MPN (cặp cạnh góc vuông tỉ lệ).
+) Tam giác MNP vuông tại M và tam giác EDF vuông tại E có:
\(\widehat P = \widehat F\)
Do đó, ∆MNP ᔕ ∆EDF (hai góc nhọn bằng nhau).
+) Tam giác ABC vuông ở A và tam giác GHK vuông ở G có:
\(\frac{{AB}}{{GH}} = \frac{{BC}}{{HK}}\) \(\left( {\frac{2}{1} = \frac{{\sqrt {13} }}{{\frac{{\sqrt {13} }}{2}}}} \right)\)
Do đó, ∆ABC ᔕ ∆GHK (ch – cgv).
Lời giải
Lời giải
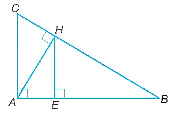
a) Vì AH là đường cao trong tam giác ABC nên AH vuông góc với BC.
Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:
\(\widehat C\) chung
Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).
Suy ra \(\frac{{AC}}{{HC}} = \frac{{BC}}{{AC}}\) nên AC2 = CH . BC.
b)
Vì HE vuông góc với AB (E thuộc AB) nên \(\widehat {AEH} = 90^\circ \).
Ta có \(\widehat {HAE} + \widehat {CAH} = \widehat {CAB} = 90^\circ \) và \(\widehat C + \widehat {CAH} = 90^\circ \) (do tam giác CAH vuông tại H).
Do đó, \(\widehat {HAE} = \widehat C\) (cùng phụ với góc CAH).
Tam giác AHE vuông ở E và tam giác CBA vuông ở A có:
\(\widehat {HAE} = \widehat C\)
Do đó, ∆AHE ᔕ ∆CBA (hai góc nhọn bằng nhau).
Suy ra: \(\frac{{AH}}{{BC}} = \frac{{HE}}{{AB}}\).
Lời giải
Lời giải
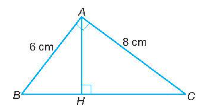
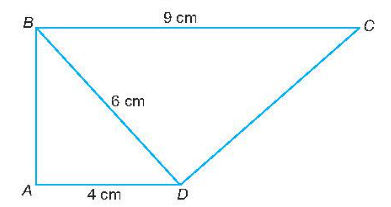
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:
BC2 = AB2 + AC2 = 62 + 82 = 100
Nên BC = 10 cm.
Vì AH là đường cao trong tam giác ABC nên AH vuông góc với BC.
Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:
\(\widehat C\) chung
Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).
Suy ra \(\frac{{AC}}{{HC}} = \frac{{BC}}{{AC}}\) nên CH = \(\frac{{C{A^2}}}{{CB}} = \frac{{{8^2}}}{{10}} = \frac{{32}}{5} = 6,4\) (cm).
Do đó, BH = BC – CH = 10 – 6,4 = 3,6 (cm).
Vì ∆ABC ᔕ ∆HAC (cmt) nên \(\frac{{AB}}{{HA}} = \frac{{BC}}{{AC}}\).
Do đó, AH = \(\frac{{AB \cdot AC}}{{BC}} = \frac{{6 \cdot 8}}{{10}} = 4,8\) (cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.