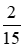Câu hỏi:
11/07/2024 1,673
Điểm số trung bình của một vận động viên bắn súng sau 100 lần bắn là 8,69 điểm. Kết quả cụ thể được ghi trong bảng sau, trong đó có hai ô bị mờ không đọc được (đánh dấu "?"):
Điểm số của mỗi lần bắn
10
9
8
7
6
Số lần bắn
25
42
?
15
?
Em hãy tìm lại các số bị mờ trong hai số đó.
Điểm số trung bình của một vận động viên bắn súng sau 100 lần bắn là 8,69 điểm. Kết quả cụ thể được ghi trong bảng sau, trong đó có hai ô bị mờ không đọc được (đánh dấu "?"):
|
Điểm số của mỗi lần bắn |
10 |
9 |
8 |
7 |
6 |
|
Số lần bắn |
25 |
42 |
? |
15 |
? |
Em hãy tìm lại các số bị mờ trong hai số đó.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi số thứ nhất bị mờ là x, số thứ hai bị mờ là y (x > 0, y > 0).
Số lần bắn là 100 nên ta có: 25 + 42 + x + 15 + y = 100 hay x + y = 18. (1)
Điểm số trung bình của một vận động viên bắn súng sau 100 lần bắn là 8,69 điểm nên ta có phương trình:
10 . 25 + 9 . 42 + 8x + 7 . 15 + 6y = 100 . 8,69
250 + 378 + 8x + 105 + 6y = 869
8x + 6y = 136
4x + 3y = 68. (2)
Từ (1) và (2), ta có hệ phương trình: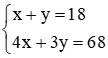 
. (I)
Nhân hai vế của phương trình thứ nhất với 3, ta được: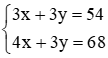 
.
Trừ từng vế hai phương trình của hệ mới, ta được –x = –14 hay x = 14 (thỏa mãn điều kiện).
Thế x = 14 vào phương trình thứ nhất của hệ (I), ta có 14 + y = 18 suy ra y = 4 (thỏa mãn điều kiện).
Vậy số thứ nhất bị mờ là 14, số thứ hai bị mờ là 4.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x (km/h), y (km/h) lần lượt là vận tốc của xe khách và xe tải (x > 0, y > 0).
Vì rằng mỗi xe khách đi nhanh hơn xe tải 15 km nên ta có x – y = 15. (1)
Đổi 1 giờ 40 phút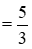 
giờ, 40 phút 
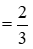giờ.
Thời gian xe khách đi được là: 
(giờ).
Quãng đường xe khách đi được là: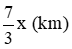 
.
Quãng đường xe tải đi được là: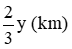 
.
Vì quãng đường Thành phố Hồ Chí Minh đến Cần Thơ dài 170 km nên ta có
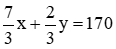. (2)
Từ (1) và (2) ta có phương trình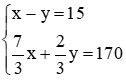 
.
Nhân hai vế của phương trình thứ hai với 7, ta được: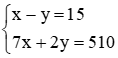 
.
Từ phương trình thứ nhất ta có y = x – 15. Thế vào phương trình thứ hai, ta được
7(x – 15) + 2y = 510, tức là 9x – 30 = 510, suy ra x = 60 (thỏa mãn điều kiện).
Từ đó y = 60 – 15 = 45 (thỏa mãn điều kiện).
Vậy vận tốc của xe khách là 45 km/h và vận tốc của xe tải là 60 km/h.
Lời giải
Gọi số cần tìm là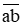 
(a, b ∈ ℕ*; 0 < a < b < 10) .
Tổng của hai chữ số bằng 12 nên ta có a + b = 12. (1)
Số ban đầu là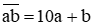 
.
Khi đổi chỗ hai chữ số thì ta được số mới là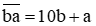 
.
Số mới lớn hơn số cũ 36 đơn vị nên ta có phương trình
10a + b + 36 = 10b + a hay 9b – 9a = 36, suy ra b – a = 4. (2)
Từ (1) và (2), ta có hệ phương trình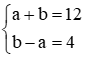 
.
Trừ từng vế hai phương trình của hệ mới, ta được 2a = 8 hay a = 4 (thỏa mãn điều kiện).
Thay a = 4 vào phương trình thứ nhất của hệ, ta có
4 + b = 12, suy ra b = 12 – 4 = 8 (thỏa mãn điều kiện).
Vậy số cần tìm là 48.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Chuyên đề 8: Hình học (có đáp án)