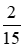Giải SGK Toán 9 KNTT Bài 3. Giải bài toán bằng cách lập hệ phương trình có đáp án
31 người thi tuần này 4.6 1.3 K lượt thi 10 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
Sau bài học này ta giải quyết được bài toán như sau:
Gọi x là số gam đồng, y là số gam kẽm cần tính (x > 0, y > 0).
Vật có khối lượng 124 g nên ta có x + y = 124. (1)
Vì 1 cm3 đồng nặng 8,9 g nên 1 g đồng có thể tích 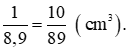
Vì 1 cm3 kẽm nặng 7 g nên 1 g kẽm có thể tích 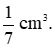
Thể tích của x (g) đồng là 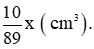
Thể tích của y (g) kẽm là 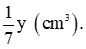
Vật có thể tích 15 cm3 nên ta có 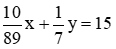 . (2)
. (2)
Từ (1) và (2) ta có hệ phương trình 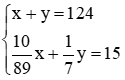 .
.
Nhân hai vế của phương trình thứ hai với 7, ta được: 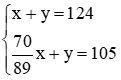 .
.
Trừ từng vế hai phương trình của hệ mới, ta được
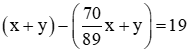 hay
hay 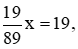 suy ra x = 89 (thỏa mãn điều kiện).
suy ra x = 89 (thỏa mãn điều kiện).
Thế x = 89 vào phương trình thứ nhất của hệ ban đầu, ta có
89 + y = 124, suy ra y = 35 (thỏa mãn điều kiện).
Vậy có 89 g đồng và 35 g kẽm.
Lời giải
Gọi x là số gam đồng, y là số gam kẽm cần tính (x > 0, y > 0).
Vật có khối lượng 124 g nên ta có x + y = 124.
Vậy biểu thức biểu thị khối lượng của vật qua x và y là: x + y = 124.
Lời giải
Gọi x là số gam đồng, y là số gam kẽm cần tính (x > 0, y > 0).
Vì 1 cm3 đồng nặng 8,9 g nên 1 g đồng có thể tích 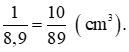
Vì 1 cm3 kẽm nặng 7 g nên 1 g kẽm có thể tích 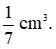
Thể tích của x (g) đồng là 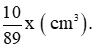
Thể tích của y (g) kẽm là 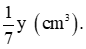
Vật có thể tích 15 cm3 nên ta có 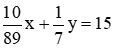 .
.
Vậy biểu thức biểu thị thể tích của vật qua x và y là 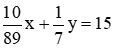 .
.
Lời giải
Từ HĐ1 và HĐ2 ta có hệ phương trình 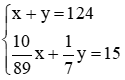 .
.
Nhân hai vế của phương trình thứ hai với 7, ta được: 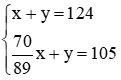 .
.
Trừ từng vế hai phương trình của hệ mới, ta được
 hay
hay  suy ra x = 89 (thỏa mãn điều kiện).
suy ra x = 89 (thỏa mãn điều kiện).
Thế x = 89 vào phương trình thứ nhất của hệ ban đầu, ta có
89 + y = 124, suy ra y = 35 (thỏa mãn điều kiện).
Vậy có 89 g đồng và 35 g kẽm.
Lời giải
Gọi x (km/h), y (km/h) lần lượt là vận tốc của xe khách và xe tải (x > 0, y > 0).
Vì rằng mỗi xe khách đi nhanh hơn xe tải 15 km nên ta có x – y = 15. (1)
Đổi 1 giờ 40 phút 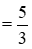 giờ, 40 phút
giờ, 40 phút 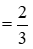 giờ.
giờ.
Thời gian xe khách đi được là:  (giờ).
(giờ).
Quãng đường xe khách đi được là: 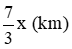 .
.
Quãng đường xe tải đi được là: 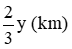 .
.
Vì quãng đường Thành phố Hồ Chí Minh đến Cần Thơ dài 170 km nên ta có
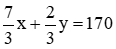 . (2)
. (2)
Từ (1) và (2) ta có phương trình 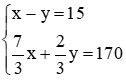 .
.
Nhân hai vế của phương trình thứ hai với 7, ta được: 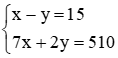 .
.
Từ phương trình thứ nhất ta có y = x – 15. Thế vào phương trình thứ hai, ta được
7(x – 15) + 2y = 510, tức là 9x – 30 = 510, suy ra x = 60 (thỏa mãn điều kiện).
Từ đó y = 60 – 15 = 45 (thỏa mãn điều kiện).
Vậy vận tốc của xe khách là 45 km/h và vận tốc của xe tải là 60 km/h.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.