Theo thuyết tương đối hẹp, khối lượng m (kg) của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức \[m(v) = \frac{{{m_o}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\], trong đó mo là khối lượng nghỉ của hạt, c = 300000 km/s là tốc độ ánh sáng. Tìm tiệm cận của đồ thị hàm số khối lượng hạt \[m(v) = \frac{{{m_o}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\] . Từ đó, có nhận xét gì khi hạt di chuyển với tốc độ càng gần tốc độ ánh sáng thì khối lượng của hạt thay đổi như thế nào?
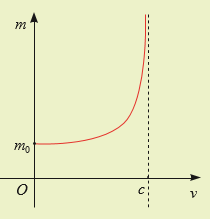
Theo thuyết tương đối hẹp, khối lượng m (kg) của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức \[m(v) = \frac{{{m_o}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\], trong đó mo là khối lượng nghỉ của hạt, c = 300000 km/s là tốc độ ánh sáng. Tìm tiệm cận của đồ thị hàm số khối lượng hạt \[m(v) = \frac{{{m_o}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\] . Từ đó, có nhận xét gì khi hạt di chuyển với tốc độ càng gần tốc độ ánh sáng thì khối lượng của hạt thay đổi như thế nào?

Quảng cáo
Trả lời:
Tập xác định: \({\rm{D}} = (0;{\rm{c}}]\).
Có \(\mathop {\lim }\limits_{v \to {c^ + }} m(v) = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = + \infty ;\mathop {\lim }\limits_{v \to c} m(v) = \mathop {\lim }\limits_{v \to c} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = + \infty \)
Do đó \(v = c\) là tiệm cận đứng của đồ thị hàm số.
Hàm số không có tiệm cận ngang.
Khi hạt di chuyến với tốc độ càng gần tốc độ ánh sáng thì khối lượng của hạt tiến gần tới vô cùng.
Trên hình điều này được thế hiện đường cong biếu diễn \(m(v)\) sẽ tiến dần đến vô cùng khi \(v \to c\). Điều này cho thấy rẳng khối lượng của hạt sẽ tăng tới vô cùng khi tốc độ di chuyến của nó tiến gân tốc độ ánh sáng.Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
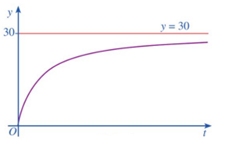
a) Sau 1 phút, ta có: khối lượng muối trong bể là 25 . 30 . t = 750t (gam); thể tích của lượng nước trong bể là 5 000 + 25t (lít). Vậy nồng độ muối sau 1 phút là \[f(t) = \frac{{750t}}{{5000 + 25t}} = \frac{{30t}}{{200 + t}}\] (gam/lít).
b) Ta có: \[\mathop {\lim }\limits_{t \to + \infty } f(t) = \mathop {\lim }\limits_{t \to + \infty } \frac{{30t}}{{200 + t}} = \mathop {\lim }\limits_{t \to + \infty } \left( {30 - \frac{{6000}}{{200 + t}}} \right) = 30\]
Vậy đường thẳng y = 30 là tiệm cận ngang của đồ thị hàm số f(t).
c) Ta có đồ thị hàm số y = f(t) nhận đường thẳng y = 30 làm tiệm cận ngang, tức là khi t càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức 30 (gam/lít). Lúc đó, nồng độ muối trong bể sẽ gần như bằng nồng độ muối trong nước muối được bơm vào bể.
Lời giải
a) Xét hàm số \(y = S(x) = 200\left( {5 - \frac{9}{{2 + x}}} \right)\) với \(x \in [1; + \infty )\).
Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } 200\left( {5 - \frac{9}{{2 + x}}} \right) = 1000;\mathop {\lim }\limits_{x \to - \infty } = 200\left( {5 - \frac{9}{{2 + x}}} \right) = 1000\).
Do đó, đường thẳng \(y = 1000\) là tiệm cận ngang của đồ thị hàm số đã cho trên nửa khoảng \([1; + \infty )\).
b) Ta có đồ thị hàm số \(y = S(x)\) với \(x \in [1; + \infty )\) nhận đường thẳng \(y = 1000\) làm tiệm cận ngang, tức là khi \(x\) càng lớn thì số lượng sản phấm bán được của công ty đó trong \({\rm{x}}\) (tháng) sẽ tiến gần đến 1000 sản phấm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.