Tiếp tuyến của đồ thị hàm số \(y = {x^3} - 2{x^2} + 3x - 1\) tại điểm có hoành độ \(x = - 1\) có hệ số góc \(k\) bằng
Tiếp tuyến của đồ thị hàm số \(y = {x^3} - 2{x^2} + 3x - 1\) tại điểm có hoành độ \(x = - 1\) có hệ số góc \(k\) bằng
Quảng cáo
Trả lời:
TXĐ: \(D = \mathbb{R}\).
Ta có \(y' = 3{x^2} - 4x + 3\).
Hệ số góc của tiếp tuyến là \(k = y'\left( { - 1} \right)\)\( = 3.{\left( { - 1} \right)^2} - 4.\left( { - 1} \right) + 3\)\( = 10\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
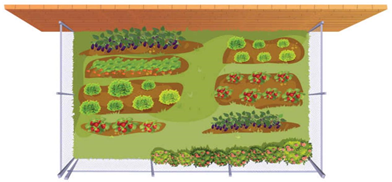
Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều rộng của khu đất hình chữ nhật cần rào.
Theo đề bài, ta có \(0 < x \le 15\).
Diện tích khu đất này là \(200\left( {{\rm{\;}}{{\rm{m}}^2}} \right)\) nên chiều dài của khu đất là \(\frac{{200}}{x}\left( {{\rm{\;m}}} \right)\).
Tổng chiều dài lưới thép rào quanh khu đất là \(L\left( x \right) = 2x + \frac{{200}}{x}\left( {{\rm{\;m}}} \right)\).
Xét hàm số: \(L\left( x \right) = 2x + \frac{{200}}{x}\), với \(x \in \left( {0;15} \right]\).
Ta có: \(L'\left( x \right) = 2 - \frac{{200}}{{{x^2}}} = \frac{{2{x^2} - 200}}{{{x^2}}}\);
\(L'\left( x \right) = 0 \Leftrightarrow x = 10({\rm{\;do\;}}x > 0){\rm{.}}\)
Ta có: 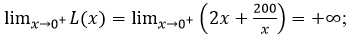
\(L\left( {10} \right) = 40\)
\(L\left( {15} \right) = \frac{{130}}{3}.\)
Bảng biến thiên:
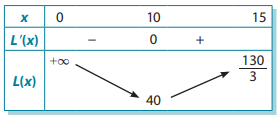
Dựa vào bảng biến thiên, chiều dài lưới thép ngắn nhất là 40m khi chiều rộng khu đất này là x = 10(m) (và chiều dài là .
Lời giải
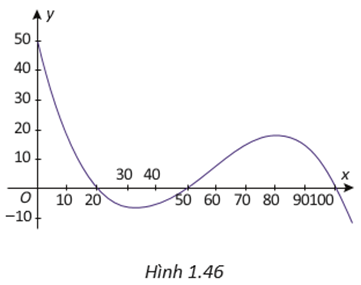
a) Do đồ thị hàm số giao với trục hoành tại các điểm x = 20; x = 50, x = 100 nên phương trình f(x) = 0 có 3 nghiệm 20, 50, 100, từ đó ta có: y = a(x – 20)(x – 50)(x – 100).
Mặt khác, tại điểm x = 0 ta có y = 50, suy ra: 50 = a(0 – 20)(0 – 50 )(0 – 100) hay a = \[ - \frac{1}{{2000}}\].
Suy ra: \[y = - \frac{1}{{2000}}\left( {x - 20} \right)\left( {x - 50} \right)\left( {x - 100} \right) = - \frac{1}{{2000}}{x^3} + \frac{{17}}{{200}}{x^2} - 4x + 50\].
b) Các điểm cần thìm chính là các điểm cực trị của hàm số: \[y = f(x) = - \frac{1}{{2000}}{x^3} + \frac{{17}}{{200}}{x^2} - 4x + 50\]
\[y' = - \frac{3}{{2000}}{x^2} + 1\frac{{17}}{{200}}x - 4 = 0 \Leftrightarrow x = \frac{{100}}{3};x = 80\]
Ta có các điểm cực trị của hàm số f(x) là \[A\left( {\frac{{10}}{3}; - \frac{{200}}{{27}}} \right);B\left( {80;18} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.