Vẽ hình minh họa và ghi giả thiết, kết luận bằng kí hiệu.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 7 Bài 11: Định lí và chứng minh định lí có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải:

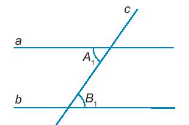
Giả thiết: c cắt a tại A, c cắt b tại B, tạo thành cặp góc so le trong \(\widehat {{A_1}};\widehat {{B_1}}\) và \(\widehat {{A_1}} = \widehat {{B_1}}\)

Kết luận: a // b.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Hai góc cùng bù với một góc thứ ba thì bằng nhau.

Xem đáp án

Lời giải

Hướng dẫn giải:

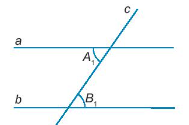
Media VietJack

Giả thiết: \(\widehat {xOy} + \widehat {uHv} = 180^\circ \);\(\widehat {x'Oy'} + \widehat {uHv} = 180^\circ \).

Kết luận: \(\widehat {xOy} = \widehat {x'Oy'}\)

Chứng minh:

Ta có: \(\widehat {xOy} + \widehat {uHv} = 180^\circ \) suy ra, \(\widehat {xOy} = 180^\circ - \widehat {uHv}\) (3)

\(\widehat {x'Oy'} + \widehat {uHv} = 180^\circ \) suy ra, \(\widehat {x'Oy'} = 180^\circ - \widehat {uHv}\) (2)

Từ (1) và (2) suy ra: \(\widehat {xOy} = \widehat {x'Oy'}\) = \(180^\circ - \widehat {uHv}\)

Vậy \(\widehat {xOy} = \widehat {x'Oy'}\)

Câu 2

Cho định lí: “Tia đối của tia phân giác của một góc là tia phân giác của góc đối đỉnh với góc đó”. Hãy vẽ hình ghi giả thiết, kết luận và chứng minh định lí đó.

Xem đáp án

Lời giải

Lời giải:

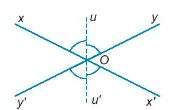
Media VietJack

Giả thiết:

- Hai góc xOy; x’Oy’ là hai góc đối đỉnh.

- Ou là tia phân giác của góc xOy, Ou’ là tia đối của tia Ou.

Kết luận: Ou’ là tia phân giác của góc x’Oy’.

Chứng minh định lí:

Ta có:

\(\widehat {x'Ou'}\) và \(\widehat {xOu}\) là hai góc đối đỉnh nên \(\widehat {x'Ou'}\) = \(\widehat {xOu}\).

\(\widehat {y'Ou'}\) và \(\widehat {yOu}\) là hai góc đối đỉnh nên \(\widehat {y'Ou'}\) = \(\widehat {yOu}\).

Lại có: Ou là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOu}\) = \(\widehat {yOu}\).

Suy ra: \(\widehat {x'Ou'}\) = \(\widehat {y'Ou'}\).

Do đó, Ou’ là tia phân giác của \(\widehat {x'Oy'}\).

Vậy Ou’ là tia phân giác của \(\widehat {x'Oy'}\) (điều phải chứng minh).

Câu 3