5 câu Trắc nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác có đáp án (Nhận biết)
60 người thi tuần này 4.6 2.4 K lượt thi 5 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 03
Danh sách câu hỏi:
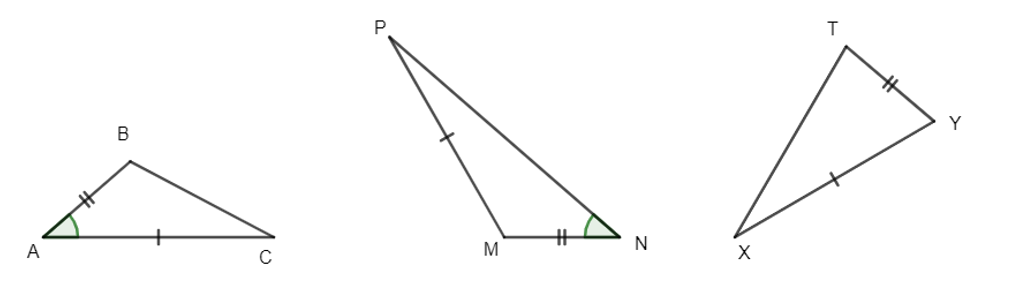
Câu 1
A. ∆ABC = ∆NMP;
B. ∆BAC = ∆MNP;
C. ∆ABC = ∆MNP;
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Xét ∆ABC và ∆NMP, có:
AB = NM (giả thiết)
AC = NP (giả thiết)
(giả thiết)
Do đó ∆ABC = ∆NMP (c.g.c)
Ta cũng có thể kí hiệu là: ∆BAC = ∆MNP hay ∆CAB = ∆PNM.
Do đó kí hiệu ở các phương án A, B, D đúng, kí hiệu ở phương án C sai.
Vậy ta chọn phương án C.
Câu 2
A. cạnh và góc;
B. góc và góc;
C. cạnh và cạnh;
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có phát biểu sau:
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Suy ra từ cần điền là cạnh và góc.
Vậy chọn đáp án A.
Câu 3
A. ∆ABC = ∆MNP;
B. ∆ABC = ∆XYT;
C. ∆MNP = ∆XYT;
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
⦁ Xét ∆ABC và ∆MNP, có:
AB = MN (giả thiết)
AC = MP (giả thiết)
(giả thiết)
Tuy nhiên hai góc và không xen giữa hai cạnh đã cho.
Suy ra ∆ABC và ∆MNP không bằng nhau. Do đó A sai.
⦁ Xét ∆MNP và ∆XYT, có:
MN = YT (giả thiết)
MP = XY (giả thiết)
Chưa đủ điều kiện để suy ra ∆MNP và ∆XYT bằng nhau. Do đó B sai.
⦁ Xét ∆ABC và ∆XYT, có:
AB = YT (giả thiết)
AC = XY (giả thiết)
Chưa đủ điều kiện để suy ra ∆ABC và ∆XYT bằng nhau. Do đó C sai.
Vì vậy không có cặp tam giác nào bằng nhau.
Vậy chọn đáp án D
Câu 4
A. N và P;
B. M và N;
C. M và P;
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Vì ∆ABC = ∆MNP (c – g – c) nên đỉnh A tương ứng với M, B tương ứng với N, C tương ứng với P.
Vậy ta chọn phương án B.
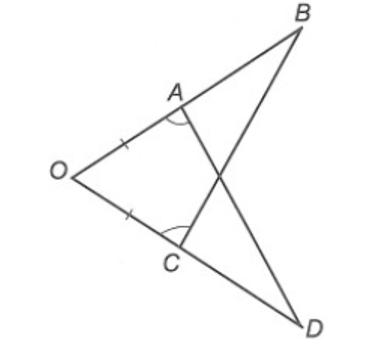
Câu 5
A. ∆OAC và ∆OBD;
B. ∆OAD và ∆OCB;
C. ∆ABC và ∆BCD;
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
⦁ Xét ∆OAD và ∆OCB, có:
(giả thiết)
OA = OC (giả thiết)
là góc chung.
Do đó ∆OAD = ∆OCB (g.c.g)
Vì vậy phương án B đúng.
⦁ Phương án A sai vì OA < OB và A ∈ OB.
⦁ Phương án C, D sai vì không có các cặp cạnh, cặp góc tương ứng thỏa mãn cả ba trường hợp bằng nhau của hai tam giác.
Vậy ta chọn phương án B.