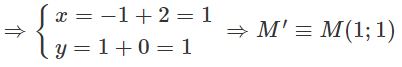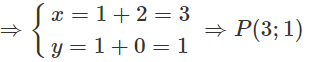Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
25 người thi tuần này 2.0 32 K lượt thi 4 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THPT Việt Đức (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Tạ Quang Bửu (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Nguyễn Bỉnh Khiêm (Hà Nội) có đáp án
Trắc nghiệm Công thức nhân xác suất cho hai biến cố độc lập lớp 11 (có đúng sai, trả lời ngắn)
Trắc nghiệm Công thức cộng xác suất lớp 11 (có đúng sai, trả lời ngắn)
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Phùng Khắc Khoan (Thạch Thất-Hà Nội) có đáp án - mã đề 0123
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Vạn Xuân (Hoài Đức-Hà Nội) có đáp án - Đề chẵn
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) M(-1;1) đối xứng qua trục Oy ta được N(-1;1).
Gọi M'(x;y) là ảnh của N(-1;1) qua phép tịnh tiến theo vectơ
b) Gọi P(x;y) là ảnh của M(1;1) qua phép tịnh tiến theo
P(3;1) đối xứng qua trục Oy ta được M"(-3;1)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi là ảnh của d qua phép quay tâm 0 góc . Vì d chứa tâm quay O nên cũng chứa O. Ngoài ra vuông góc với d nên có phương trinh: 9x + 2y = 0.
Gọi d' là ảnh của qua phép tịnh tiến vectơ v. Khi đó phương trình của d' có dạng x + 2y + C = 0. Vì d' chứa O′(3;1) là ảnh của O qua phép tịnh tiến vectơ v nên 3 + 2 + C = 0 từ đó C = -5. Vậy phương trình của d' là x + 2y – 5 = 0.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
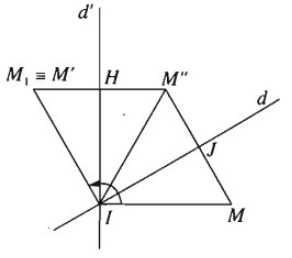
Gọi là phép quay tâm I góc α . Lấy đường thẳng d bất kì qua I. Gọi d' là ảnh của d qua phép quay tâm I góc α/2. Lấy điểm M bất kì và gọi M′ = (M). Gọi M" là ảnh của M qua phép đối xứng qua trục d. M1 là ảnh của M" qua phép đối xứng qua trục d'. Gọi J là giao của MM" với d, H là giao của M″M1 với d'. Khi đó ta có đẳng thức giữa các góc lượng giác sau:
(IM, IM1) = (IM, IM′′) + (IM′′, IM1)
= 2(IJ, IM′′) + 2(IM′′, IH)
= 2(IJ, IH)
= 2α/2 = a = (IM, IM′)
Từ đó suy ra M′ ≡ M1. Như vậy M' có thể xem là ảnh của sau khi thực hiện liên tiếp hai phép đối xứng qua hai trục d và d'.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
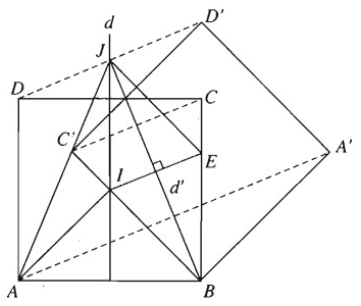
Gọi F là phép đối xứng qua đường trung trực d của cạnh AB, G là phép đối xứng qua đường trung trực d' của cạnh IE. Khi đó F biến AI thành BI, G biến BI thành BE. Từ đó suy ra phép dời hình có được bằng cách thực hiện liên tiếp hai phép biến hình F và G sẽ biến AI thành BE.
Hơn nữa gọi J là giao của d và d', thì dễ thấy JA = JB, JI = JE và 2(JI, JB) = (JI, JE) =
(vì JE / /IB). Do đó theo kết quả của bài 1.21, phép dời hình nói trên chính là phép quay tâm J góc
Lưu ý. Có thể tìm được nhiều phép dời hình biến AI thành BE.
b) F biến các điểm A, B, C, D thành B, A, D, C; G biến các điểm B, A, D, C thành B, A', D', C'. Do đó ảnh của hình vuông ABCD qua phép dời hình nói trên là hình vuông BA'D'C' đối xứng với hình vuông BADC qua d'
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập