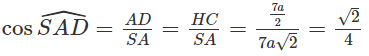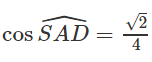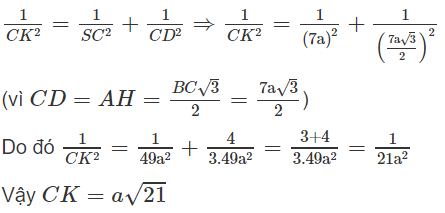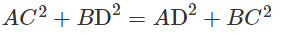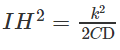Câu hỏi ôn tập chương 3

a) Đúng

b) Đúng

c) Sai

d) Sai

e) Sai

f) Đúng

a) Sai

b) Sai

c) Đúng

d) Sai

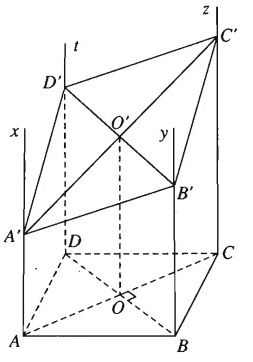
a) Ta có hai mặt phẳng song song là: (Ax, AD) // (By, BC)

Hai mặt phẳng này bị cắt bởi mặt phẳng (β) nên ta suy ra các giao tuyến của chúng phải song song nghĩa là A′D′ // B′C′.

Tương tự ta chứng minh được A′B′ // D′C′. Vậy A', B', C', D' là hình bình hành. Các hình thang AA'C'C và BB'D'D đều có OO' là đường trung bình trong đó O là tâm của hình vuông ABCD và O' là tâm của hình bình hành A',B',C',D'. Do đó: AA′ + CC′ = BB′ + DD′ = 2OO′

b) Muốn hình bình hành A',B',C',D' là hình thoi ta cần phải có A'C' ⊥ B'D'. Ta đã có AC ⊥ BD. Người ta chứng minh được rằng hình chiếu vuông góc của một góc vuông là một góc vuông khi và chỉ khi góc vuông đem chiếu có ít nhất một cạnh song song với mặt phẳng chiếu hay nằm trong mặt chiếu. Vậy A', B', C', D' là hình thoi khi và chỉ khi A'C' hoặc B'D' song song với mặt phẳng (α) cho trước. Khi đó ta có AA' = CC' hoặc BB' = DD'.

c) Muốn hình bình hành A', B', C', D' là hình chữ nhật ta cần có A'B' ⊥ B'C', nghĩa là A'B' hoặc B'C' phải song song với mặt phẳng (α)(α). Khi đó ta có AA' = BB' hoặc BB' = CC', nghĩa là hình bình hành A', B', C', D' có hai đỉnh kề nhau cách đều mặt phẳng (α) cho trước.

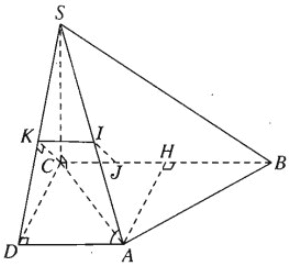
a) Gọi H là trung điểm của đoạn BC. Qua A vẽ AD song song với BC và bằng đoạn HC thì góc giữa BC và SA là góc ∠SAD. Theo định lí ba đường vuông góc, ta có SD ⊥ DA và khi đó:

Vậy góc giữa BC và SA được xác định sao cho 

Vì BC // AD nên BC song song với mặt phẳng (SAD). Do đó khoảng cách giữa SA và BC chính là khoảng cách từ đường thẳng BC đến mặt phẳng (SAD).

Ta kẻ CK ⊥ SD, suy ra CK ⊥ (SAD), do đó CK chính là khoảng cách nói trên. Xét tam giác vuông SCD với đường cao CK xuất phát từ đỉnh góc vuông C ta có hệ thức:

Chú ý. Nếu kẻ KI // AD và kẻ IJ // CK thì IJ là đoạn vuông góc chung của SA và BC.

Giả sử AB ⊥ CD ta phải chứng minh:

Thật vậy, kẻ BE ⊥ CD tại E, do AB⊥CD ta suy ra CD ⊥ (ABE) nên CD ⊥ AE. Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:

Nếu $A{C}^2 - A{D}^2 = B{C}^2 - B{D}^2 = k^2$ thì trong mặt phẳng (ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho 

Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên. Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD ⊥ AB.

Nếu $A{C}^2 - A{D}^2 = B{C}^2 - B{D}^2 =- k^2$ thì ta có và đưa về trường hợp xét như trên $A{C}^2 - A{D}^2 = B{C}^2 - B{D}^2 = -k^2$.

Chú ý. Từ kết quả của bài toán trên ta suy ra:

Tứ diện ABCD có các cặp cạnh đối diện vuông góc với nhau khi và chỉ khi $A{B}^2 + C{D}^2 = A{C}^2 + B{C}^2$.