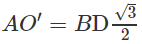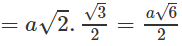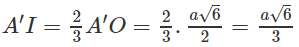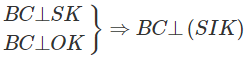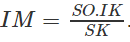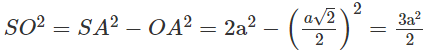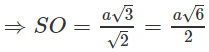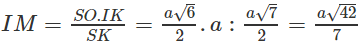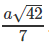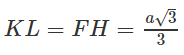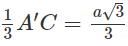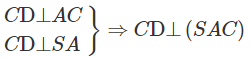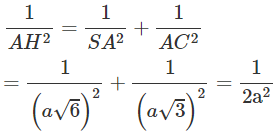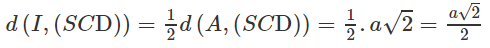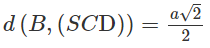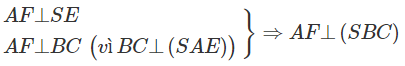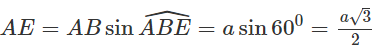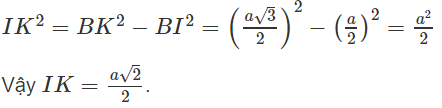Bài 5: Khoảng cách

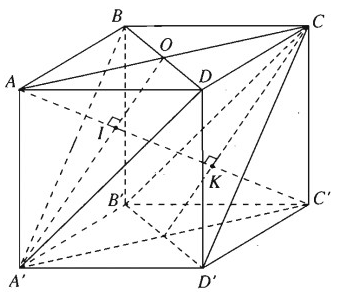
Điểm A cách đều ba đỉnh của tam giác đều A'BD vì ta có AB = AD = AA′ = a, điểm C' cũng cách đều ba đỉnh của tam giác đều đó vì ta có:

C′B = C′D = C′A′ = a√2

Vậy AC' là trục của đường tròn ngoại tiếp tam giác A'BD, tức là đường thẳng AC' vuông góc với mặt phẳng (A'BD) tại trọng tâm I của tam giác A'BD. Ta cần tìm khoảng cách A'I.

Ta có A′I = BI = DI = 2A′O/3 với O là tâm của hình vuông ABCD

Ta lại có 

Vậy 

Tương tự điểm C' cách đều ba đỉnh của tam giác đều CB'D', tính được khoảng cách từ C, B', D' tới đường chéo AC'.

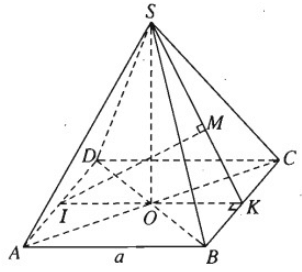
a) Gọi O là tâm hình vuông ABCD , dễ thấy I, O, K thẳng hàng. Vì K là trung điểm của BC nên SK ⊥ BC.

Ta có 

Do đó (SBC) ⊥ (SIK)

b) Hai đường thẳng AD và SB chéo nhau. Ta có mặt phẳng (SBC) chứa SB và song song với AD. Do đó khoảng cách giữa AD và SB bằng khoảng cách giữa AD và mặt phẳng (SBC).

Theo câu a) ta có (SIK) ⊥ (SBC) theo giao tuyến SK và khoảng cách cần tìm là IM, trong đó M là chân đường vuông góc hạ từ I tới SK. Dựa vào hệ thức IM. SK = SO. IK

ta có 

Ta lại có:

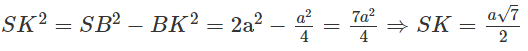
Do đó:

Vậy khoảng cách giữa hai đường thẳng AD và SB là bằng 

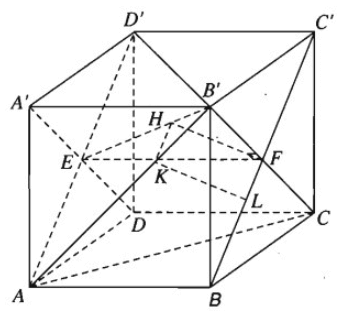
a) Ta có B'C ⊥ BC' vì đây là hai đường chéo của hình vuông BB'C'C

Ngoài ra ta còn có: A'B' ⊥ (BB'C'C) ⇒ A'B' ⊥ BC'

Từ đó ta suy ra BC' ⊥ (A'B'CD) vì mặt phẳng (A'B'CD) chứa đường thẳng A'B' và B'C cùng vuông góc với BC'.

b) Mặt phẳng (AB'D') chứa đường thẳng AB' và song song với BC', ta hãy tìm hình chiếu của BC' trên mặt phẳng (AB'D'). Gọi E, F lần lượt là tâm các hình vuông ADD'A', BCC'B'. Kẻ FH ⊥ EB'với H ∈ EB', khi đó FH nằm trên mặt phẳng (A'B'CD) nên theo câu a) thì FH ⊥ (AB'D'), do đó hình chiếu BC' trên mặt phẳng (AB'D) là đường thẳng đi qua H và song song với BC'. Giả sử đường thẳng đó cắt AB' tại K thì từ K vẽ đường thẳng song song với FH cắt BC' tại L. Khi đó KL là đoạn vuông góc chung cần dựng. Tam giác B'EF vuông tại F nên từ công thức 

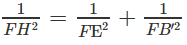
ta tính được 

Nhận xét . Độ dài đoạn vuông góc chung của AB' và BC' bằng khoảng cách giữa hai mặt phẳng song song (AB'D') và (BC'D) lần lượt chứa hai đường thẳng đó.

Khoảng cách này bằng 

a) Vì ABCD là nửa lục giác đều nội tiếp trong đường tròn đường kính AD = 2a nên ta có: AD //BC và AB = BC = CD = a, đồng thời AC ⊥ CD, AB ⊥ BD, AC = BD = a√3.

Như vậy 

Trong mặt phẳng (SAC) dựng AH ⊥ SC tại H ta có AH ⊥ CD và AH ⊥ SC nên AH ⊥ (SCD)

Vậy AH = d(A,(SCD))

Xét tam giác SAC vuông tại A có AH là đường cao, ta có:

Vậy $A{H}^2 = 2a^2 \Rightarrow AH = a\sqrt{2}$

Gọi I là trung điểm của AD ta có BI // CD nên BI song song với mặt phẳng (SCD). Từ đó suy ra d(B, (SCD)) = d(I,(SCD)).

Mặt khác AI cắt (SCD) tại D nên

Do đó: 

b) Vì AD // BC nên AD // (SBC), do đó d(AD, (SBC)) = d(A,(SBC))

Dựng AD ⊥ BC tại E ⇒ BC ⊥ (SAE)

Dựng AD ⊥ SE tại F ta có:

Vậy AF = d(A,(SBC)) = d(AD, (SBC))

Xét tam giác vuông AEB ta có:

Xét tam giác SAE vuông tại A ta có:

Giả thiết cho ABCD là tứ diện đều nên các cặp cạnh đối diện của tứ diện đó có vai trò như nhau. Do đó ta chỉ cần tính khoảng cách giữa hai cạnh AB và CD là đủ.

Gọi I và K lần lượt là trung điểm của AB và CD. Dễ thấy IK là đoạn vuông góc chung của AB và CD nên nó chính là khoảng cách giữa AB và CD.

Tam giác BKI vuông tại I. Ta có :