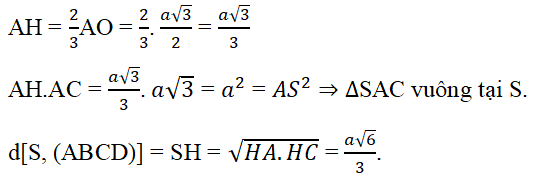Đề toán tổng hợp chương 3
20 người thi tuần này 2.0 32 K lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THPT Việt Đức (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Tạ Quang Bửu (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Nguyễn Bỉnh Khiêm (Hà Nội) có đáp án
Trắc nghiệm Công thức nhân xác suất cho hai biến cố độc lập lớp 11 (có đúng sai, trả lời ngắn)
Trắc nghiệm Công thức cộng xác suất lớp 11 (có đúng sai, trả lời ngắn)
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Phùng Khắc Khoan (Thạch Thất-Hà Nội) có đáp án - mã đề 0123
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Vạn Xuân (Hoài Đức-Hà Nội) có đáp án - Đề chẵn
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
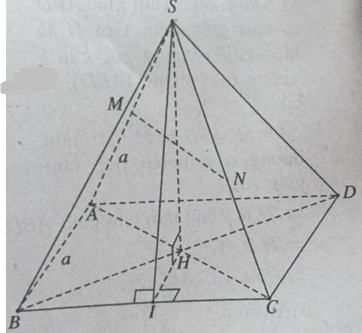
a) (AC ⊥ SH & AC ⊥ BD ⇒ AC ⊥ (SBD) ⇒ AC ⊥ SD.
b) (MN//AC & AC ⊥ (SBD) ⇒ MN ⊥ (SBD).
c) + Xác định góc α giữa (SBC) và (ABCD)
Gọi I là trung điểm của BC, ta có:
(BC ⊥ IH & BC ⊥ SH ⇒ BC ⊥ (SIH)
⇒ BC ⊥ SI.
⇒ [((SBC),(ABCD)) ] = ∠(SIH) = α.
+ Tính α:
Trong tam giác SIH, ta có: cosα = IH/IS = √3/3 ⇒ α = arccos√3/3.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
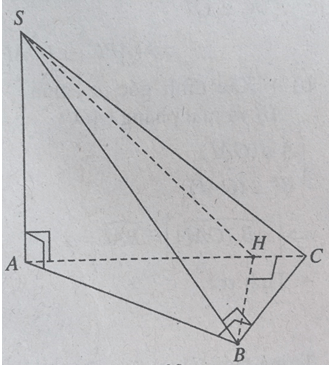
a) BC ⊥ SA & BC ⊥ AB) ⇒ BC ⊥ (SAB)
⇒ BC ⊥ SB.
⇒ tam giác SBC vuông tại B.
b) BH ⊥ AC & BH ⊥ SA ⇒ BC ⊥ (SAC)
⇒ (SBH) ⊥ (SAC).
c) d[B, (SAC)] = BH. Ta có:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
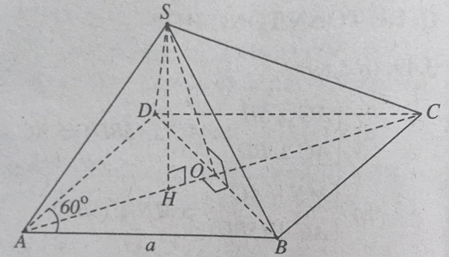
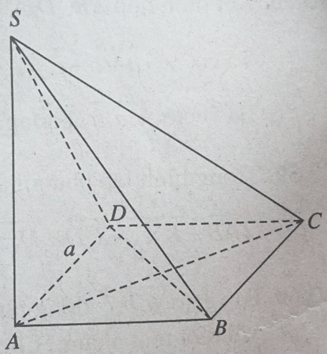
a) Nhận xét: Tam giác ABD là tam giác đều. Gọi H là hình chiếu vuông góc của S xuống mặt phẳng (ABD), ta có:
Hình 3.91
SA = SB = SD ⇒ H là tâm đường tròn ngoại tiếp tam giác ABD
⇒ H là trọng tâm tam giác ABD
⇒ H ∈ AC.
⇒ (SAC) ⊥ (ABCD).
b) Ta có:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
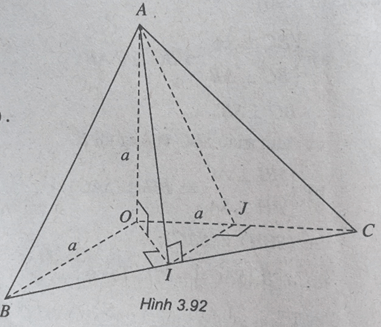
a) (BC ⊥ OA & BC ⊥ OI ⇒ BC ⊥ (OAI)
⇒ (ABC) ⊥ (OAI).
b) + Xác định góc α giữa AB và mặt phẳng (AOI)
(A ∈ (OAI) & BI ⊥ (OAI) ⇒ ∠[(AB,(OAI))] = ∠(BAI) = α.
+ Tính α:
Trong tam giác vuông BAI, ta có: sinα = 1/2 ⇒ α = 30o.
c) Xác định góc β giữa hai đường thẳng AI và OB:
Gọi J là trung điểm OC,
ta có: IJ // OB và IJ ⊥ (AOC). Như vậy:
∠[(AB,OB)] = ∠[(AI,IJ)] = ∠(AIJ) = β.
+ Tính góc:
Trong tam giác IJA,
ta có: tan β = AJ/IJ = √5 ⇒ β = arctan√5.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) (BD ⊥ SA & BD ⊥ AC ⇒ BD ⊥ (SAC)
⇒ BC ⊥ SC.
b) (BC ⊥ SA & BC ⊥ AB ⇒ BC ⊥ (SAB)
⇒ (SBC) ⊥ (SAB).
c) + Xác định góc α giữa đường thẳng SC và mp(ABCD):
(C ∈(ABCD) & SA ⊥ (ABCD) ⇒ ∠[(SC,(ABCD))] = ∠(ACS) = α
+ Tính góc:
Tam tam giác vuông SCA, ta có:
tanα = SA/AC = √3/3 ⇒ .
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập