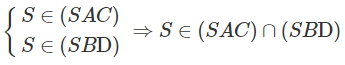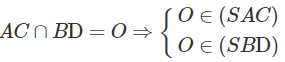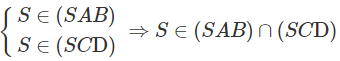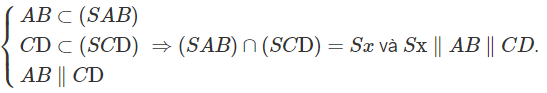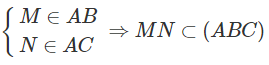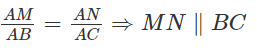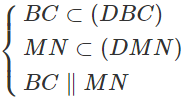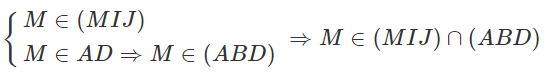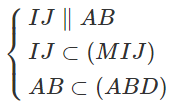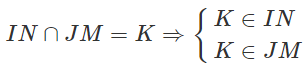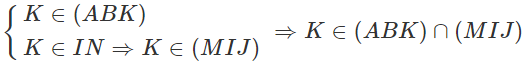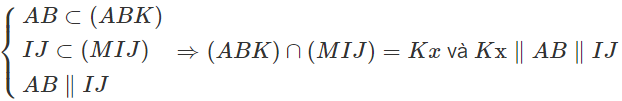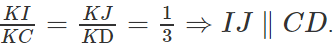Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
26 người thi tuần này 2.0 30.2 K lượt thi 6 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bài tập Vận dụng đạo hàm cấp hai để giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)
Bài tập Vận dụng các quy tắc tính đạo hàm để giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)
Bài tập Vận dụng định nghĩa đạo hàm vào giải quyết một số bài toán thực tiễn lớp 11 (có lời giải)
Bài tập Các bài toán thực tiễn vận dụng công thức nhân xác suất lớp 11 (có lời giải)
Bài tập Biến cố độc lập lớp 11 (có lời giải)
Danh sách câu hỏi:
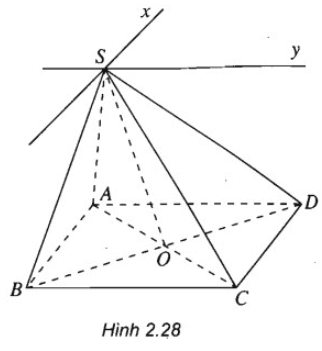
Lời giải
a)
Ta có:
Giả sử:
⇒ O ∈ (SAC) ∩ (SBD)
⇒ (SAC) ∩ (SBD) = SO
b) Ta có:
Ta lại có
c) Lập luận tương tự câu b) ta có ⇒ (SAD) ∩ (SBC) = Sy và Sy // AD // BC.
Lời giải
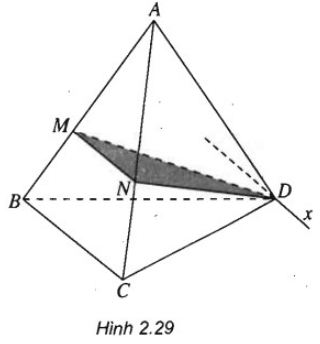
Trong tam giác ABC ta có:
Hiển nhiên D ∈ (DBC) ∩ (DMN)
⇒ (DBC) ∩ (DMN) = Dx ⇒ (DBC) ∩ (DMN) = Dx và DC // BC // MN
Lời giải
a)
Ta cũng có:
⇒ (MIJ) ∩ (ABD) = d = Mt và Mt // AB // IJ
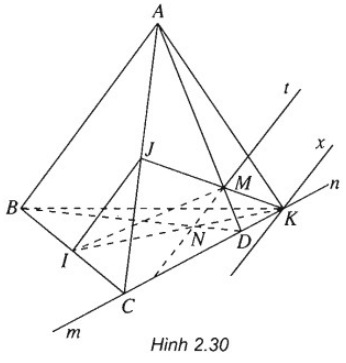
b) Ta có: Mt // AB ⇒ Mt ∩ BD = N
Vì K ∈ IN ⇒ K ∈ (BCD)
Và K ∈ JM ⇒ K ∈ (ACD)
Mặt khác (BCD) ∩ (ACD) = CD do đó K ∈ CD. Do vậy K nằm trên hai nửa đường thẳng Cm và Dn thuộc đường thẳng CD. ( Để ý rằng nếu M là trung điểm của AD thì sẽ không có điểm K.)
c) Ta có:
Mà
Lời giải
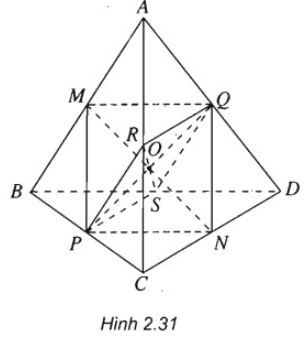
Trong tam giác ABC ta có:
MP // AC và MP = AC/2.
Trong tam giác ACD ta có:
QN // AC và QN = AC/2.
Từ đó suy ra {MP // QN}
⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = AB/2. Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
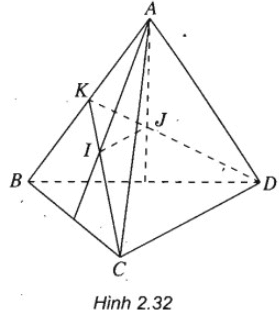
Lời giải
Gọi K là trung điểm của AB.
Vì I là trọng tâm của tam giác ABC nên I ∈ KC và vì J là trọng tâm của tam giác ABD nên J ∈ KD.
Từ đó suy ra
Lời giải
a) Ta có: I ∈ (SAD) ⇒ I ∈ (SAD) ∩ (IBC)
Vậy
Và PQ //AD // BC (1)
Tương tự: J ∈ (SBC) ⇒ J ∈ (SBC) ∩ (JAD)
Vậy
Từ (1) và (2) suy ra PQ // MN.
b) Ta có:
Do đó: EF = (AMND) ∩ (PBCQ)
Mà
Tính
EF: CP ∩ EF = K ⇒ EF = EK + KF
Từ (∗) suy ra
Tương tự ta tính được KF = 2a/5
Vậy: 
Nhắn tin Zalo
Hỏi bài tập