Câu hỏi:

13/07/2024 1,518

Một chung cư có 20 tầng và 01 tầng hầm (tầng trệt được đặt là tầng G, các tầng được đánh số từ tầng 1, 2, 3, …, 12, 12A, 14, 15, …19) tầng cao nhất đang tầng 19, tầng hầm được đánh số B1. Thang máy hiện tại đang ở tầng 10, sau đó đi lên 6 tầng và xuống 17 tầng rồi lên 01 tầng. Hỏi cuối cùng thang máy dừng lại ở tầng nào.

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 1: Nhân đa, đơn thức có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

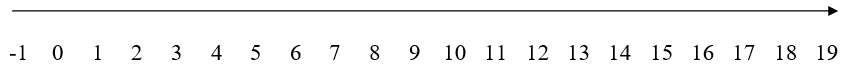
Media VietJack

+) Trục số ở trên biểu diễn các tầng của thang máy với tầng G là gốc 0,

Tầng 1, 2, 3, … 12, 12A, 14, 15, … 19 tương ứng là các số nguyên từ 1 đến 19, Tầng hầm tương ứng với -1.

+) Chiều thàng máy đi lên là +, chiều đi xuống là -.

+) Theo bài ra cuối cùng thang máy dừng ở tầng:

$10 + (+ 6) + (- 17) + (+ 1) = 0$

Vậy cuối cùng thang máy dừng ở tầng G.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Người ta muốn rào quanh một khu đất với một số vật liệu cho trước là 80 mét. Ở đó người ta tận dụng một hàng rào đã có sẵn để làm một cạnh của hàng rào và rào thành mảnh đất hình chữ nhật. Hỏi mảnh đất hình chữ nhật được rào có diện tích lớn nhất bằng bao nhiêu?

Xem đáp án

Lời giải

+) Gọi x là độ dài của cạnh song song với hàng rào đã có sẵn $(x > 0)$

Và y là độ dài của cạnh vuông góc với hàng rào đã có sẵn $(y > 0)$

Theo bài ra ta có: $x + 2 y = 80$

+) Diện tích của mảnh đất $S = x . y$

$\Leftrightarrow S = (80 - 2 y) y \Leftrightarrow S = 80 y - 2 y^{2}$

$\Leftrightarrow S = - 2 y^{2} + 2.2.20 y - 800 + 800 \Leftrightarrow S = 800 - 2 {(y - 20)}^{2} \leq 800$ .

Dấu “=” xảy ra khi và chỉ khi $y - 20 = 0 \Leftrightarrow y = 20$ .

Với $y = 20 \Rightarrow x = 40$

Vậy diện tích lớn nhất của khu đất bằng 800m² với chiều dài bằng 40m, chiều rộng bằng 20m.

Câu 2

Tìm các số nguyên a và b để đa thức $A (x) = x^{4} - 3 x^{3} + a x + b$ chia hết cho đa thức $B (x) = x^{2} - 3 x + 4$

Xem đáp án

Lời giải

Cách 1: Phương pháp thực hiện phép chia

Ta có:

Media VietJack

$\Rightarrow (x^{4} - 3 x^{3} + a x + b) : (x^{2} - 3 x + 4) = x^{2} - 4$ dư $a x - 12 x + b + 16$ .

Để là phép chia hết thì $\{\begin{cases} a - 12 = 0 \\ b + 16 = 0 \end{cases} \Leftrightarrow \{\begin{cases} a = 12 \\ b = - 16 \end{cases}$

Vậy với $a = 12$ và $b = - 16$ thì phép chia là phép chia hết

Cách 2: Phương pháp hệ số bất định

Giả sử đa thức $(x^{4} - 3 x^{3} + a x + b)$ chia hết cho $(x^{2} - 3 x + 4)$ , khi đó ta được thương là nhị thức bậc hai có dạng: $A x^{2} + B x + C$ . Nhân thương với số chia rồi đồng nhất thức với đa thức $(x^{4} - 3 x^{3} + a x + b)$ , ta được:

$(A x^{2} + B x + C) (x^{2} - 3 x + 4) = x^{4} - 3 x^{3} + a x + b$

$\Leftrightarrow A x^{4} + B x^{3} + C x^{2} - 3 A x^{3} - 3 B x^{2} - 3 C x + 4 A x^{2} + 4 B x + 4 C = x^{4} - 3 x^{3} + a x + b$

$\Leftrightarrow A x^{4} + (B - 3 A) x^{3} + (C - 3 B + 4 A) x^{2} + (4 B - 3 C) x + 4 C = x^{4} - 3 x^{3} + a x + b$

$\Leftrightarrow \{\begin{cases} A = 1 \\ B - 3 A = - 3 \\ C - 3 B + 4 A = 0 \\ 4 B - 3 C = a \\ 4 C = b \end{cases} \Leftrightarrow \{\begin{cases} A = 1 \\ B = 0 \\ C = - 4 \\ 12 = a \\ - 16 = b \end{cases} \Leftrightarrow \{\begin{cases} a = 12 \\ b = - 16 \end{cases}$

Vậy với a = 12 và b = -16 thì phép chia là phép chia hết.

Câu 3

Tìm x biết:

$x^{3} - 3 x^{2} + 3 x - 1 = 0$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm một đa thức bậc ba, biết P(x) chia cho (x - 1), (x - 2), (x - 3) đều được dư 6 và .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Phân tích đa thức thành nhân tử

$x^{3} - 5 x^{2} + 8 x - 4$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho $x + y = 1$ . Tính giá trị biểu thức sau:

$A = x^{3} + y^{3} + 3 x y (x^{2} + y^{2}) + 6 x^{2} y^{2} (x + y)$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Tìm các giá trị nguyên của x để giá trị của đa thức chia hết cho giá trị của đa thức B = x + 3.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Tìm các số nguyên a và b để đa thức Ax=x4−3x3+ax+b chia hết cho đa thức Bx=x2−3x+4

Tìm x biết: x3−3x2+3x−1=0

Tìm một đa thức bậc ba, biết P(x) chia cho (x - 1), (x - 2), (x - 3) đều được dư 6 và .

Phân tích đa thức thành nhân tử x3−5x2+8x−4

Cho x+y=1. Tính giá trị biểu thức sau: A=x3+y3+3xyx2+y2+6x2y2x+y

Tìm các giá trị nguyên của x để giá trị của đa thức chia hết cho giá trị của đa thức B = x + 3.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Tìm các số nguyên a và b để đa thức $A (x) = x^{4} - 3 x^{3} + a x + b$ chia hết cho đa thức $B (x) = x^{2} - 3 x + 4$

Tìm x biết:

$x^{3} - 3 x^{2} + 3 x - 1 = 0$

Phân tích đa thức thành nhân tử

$x^{3} - 5 x^{2} + 8 x - 4$

Cho $x + y = 1$ . Tính giá trị biểu thức sau:

$A = x^{3} + y^{3} + 3 x y (x^{2} + y^{2}) + 6 x^{2} y^{2} (x + y)$