Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 3: Hình thang cân có đáp án !!
Quảng cáo
Trả lời:
b) Do ABC là tam giác cân nên AB = AC, mà MB = DC ( = CN) nên AM = AD
=> AMD cân tại A =>
Xét ABC có: => => MD // BC => MDCB là hình thang.
Do (ABC cân tại A) => BMDC là hình thang cân. (đpcm)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
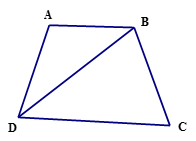
a) Ta có : ABCD là hình thang cân nên
; Tam giác CBD vuông tại B có => BC = DC hay 2AD = DC ;
AB // CD nên => ADB cân tại A nên AD = AB
Từ đó suy ra chu vi hình thang bằng 5AD => 5.AD = 20cm => AD = 4cm.
Vậy AD = AB = BC = 4cm, CD = 8cm
Lời giải
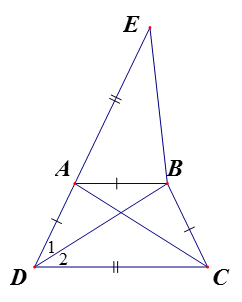
a) Trên tia DA lấy điểm E sao cho AE = CD.
Do (gt) suy ra (cùng bù với )
Từ đây ta được
cân tại B
Vậy tia DB là phân giác của góc D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.