Câu hỏi:

11/07/2024 661

Cho đoạn thẳng AB và n điểm $O_{1}, O_{2}, ..., O_{n}$ không nằm giữa A và B sao cho $O_{1} A + O_{2} A + ... + O_{n} A = O_{1} B + O_{2} B + ... + O_{n} B = a$ . Chứng minh rằng tồn tại một điểm M sao cho $O_{1} M + O_{2} M + ... + O_{n} M \leq a .$

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 5: Đường trung bình của tam giác, của hình thang có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi M là trung điểm của AB và O là một điểm tùy ý không nằm giữa A và B.

- Trường hợp O nằm trên tia đối của tia AB hay tia đối của tia BA (h.3.16), ta chứng minh được $O M = \frac{O A + O B}{2} . (1)$

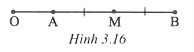
Cho đoạn thẳng AB và n điểm O1, O2, ....,On không nằm giữa A và B sao cho O1A + O2A +... + OnA = O1B + O2B +... +OnB = a. C (ảnh 1)

- Trường hợp O không thẳng hàng với A và B (h.3.17).

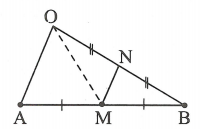
Cho đoạn thẳng AB và n điểm O1, O2, ....,On không nằm giữa A và B sao cho O1A + O2A +... + OnA = O1B + O2B +... +OnB = a. C (ảnh 2)

Gọi N là trung điểm của OB, khi đó MN là đường trung bình của $Δ O A B, M N = \frac{O A}{2}$ .

Xét $Δ O M N$ , ta có: $O M < M N + O N$

$\Rightarrow O M < \frac{O A + O B}{2} . (2)$

Từ (1) và (2) suy ra: $O M \leq \frac{O A + O B}{2} . (*)$

Áp dụng hệ thức (*) đối với n điểm $O_{1}, O_{2}, \dots, O_{n}$ ta có:

$O_{1} M \leq \frac{O_{1} A + O_{1} B}{2}; O_{2} M \leq \frac{O_{2} A + O_{2} B}{2}; \dots; O_{n} M \leq \frac{O_{n} A + O_{n} B}{2} .$

Cộng từng vế các bất đẳng thức trên ta được:

$O_{1} M + O_{2} M + \dots O_{n} M \leq \frac{O_{1} A + O_{1} B}{2} + \frac{O_{2} A + O_{2} B}{2} + \dots + \frac{O_{n} A + O_{n} B}{2} = \frac{O_{1} A + O_{2} A + \dots + O_{n} A}{2} + \frac{O_{1} B + O_{2} B + \dots + O_{n} B}{2} = \frac{a}{2} + \frac{a}{2} = a$

Như vậy điểm cần tìm chính là trung điểm M của AB.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E. Gọi M, N lần lượt là trung điểm của BE và CD. Đường thẳng MN cắt tia AB và AC lần lượt là tại P và Q. Hỏi hai điểm D và E phải có điều kiện gì để tam giác APQ cân tại A?

Xem đáp án

Lời giải

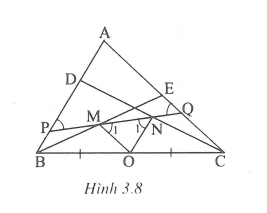
Cho tam giác ABC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E. Gọi M, N lần lượt là trung điểm của BE và CD. (ảnh 1)

Gọi O là trung điểm của BC.

Xét $Δ E B C$ có OMlà đường trung bình

=> OM // CE và $O M = \frac{C E}{2}$ .

Xét $Δ D B C$ có ON là đường trung bình

=> ON // BD và $O N = \frac{B D}{2}$ .

Ta có: $\hat{M_{1}} = \hat{A Q P}, \hat{N_{1}} = \hat{A P Q}$ (so le trong).

$Δ A P Q$ cân tại $A \Leftrightarrow \hat{Q} = \hat{P} \Leftrightarrow \hat{N_{1}} = \hat{M_{1}} \Leftrightarrow O M = O N \Leftrightarrow C E = B D$ .

Câu 2

Cho tam giác ABC, trực tâm H. Gọi O là giao điểm của ba đường trung trực. Chứng minh rằng khoảng cách từ O đến BC bằng nửa độ dài AH.

Xem đáp án

Lời giải

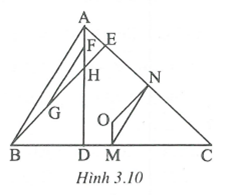
Cho tam giác ABC, trực tâm H. Gọi O là giao điểm của ba đường trung trực. Chứng minh rằng khoảng cách từ O đến BC bằng nửa độ dài AH. (ảnh 1)

Gọi M và N lần lượt là trung điểm của BC và CA.

Gọi F và G lần lượt là trung điểm của AH và BG.

Ta có MN là đường trung bình của $Δ A B C$ , FG là đường trung bình của $Δ A B H$ .

Suy ra MN // AB và $M N = \frac{1}{2} A B$

FG = AB và $F G = \frac{1}{2} A B$ .

Do đó MN // FG và MN = FG. Dễ thấy $O M // A D, O N // B E$ .

$Δ O M N$ và $Δ H F G$ có: $M N = F G; \hat{O M N} = \hat{H F G}; \hat{O N M} = \hat{H G F}$ (hai góc có cạnh tương ứng song song).

Vậy $Δ O M N = Δ H F G (g.c.g) \Rightarrow O M = H F = \frac{A H}{2}$ .

Câu 3