Câu hỏi:
14/10/2022 334
Cho tam giác nhọn ABC. Lấy M bất kì trên cạnh BC. Gọi E, F lần lượt là các điểm đối xứng vói M qua AB và AC. Gọi I, K là giao điểm của EF với AB và AC.
a) Chứng minh rằng MA là tia phân giác của .
Cho tam giác nhọn ABC. Lấy M bất kì trên cạnh BC. Gọi E, F lần lượt là các điểm đối xứng vói M qua AB và AC. Gọi I, K là giao điểm của EF với AB và AC.
a) Chứng minh rằng MA là tia phân giác của .
Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 7: Đối xứng trục có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
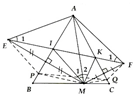
a) Sử dụng tính chất đối xứng trục kết hợp với chứng minh tam giác bằng nhau ta có được và , mà (Tính chất tam giác cân)
=> ĐPCM.
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
b) Khi M cố định, tìm vị trí điểm P AB và Q AC để chu vi tam giác MPQ đạt giá trị nhỏ nhất.
b) Khi M cố định, tìm vị trí điểm P AB và Q AC để chu vi tam giác MPQ đạt giá trị nhỏ nhất.
Xem đáp án »
13/07/2024
1,373
Câu 3:
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C. Chứng minh AC + CB < AM + MB.
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C. Chứng minh AC + CB < AM + MB.
Xem đáp án »
13/07/2024
304
Câu 5:
Cho tam giác ABC, có = 60°, trực tâm H. Gọi M là điểm đối xứng với H qua BC.
a) Chứng minh BHC = BMC
Cho tam giác ABC, có = 60°, trực tâm H. Gọi M là điểm đối xứng với H qua BC.
a) Chứng minh BHC = BMC
Xem đáp án »
14/10/2022
246
Câu 6:
Cho tam giác ABC có AB < AC, gọi d là đường trung trực của BC. Vẽ K đối xứng với A qua d.
a) Tìm đoạn thẳng đối xứng với đoạn thẳng AB qua đường thẳng d; tìm đoạn thẳng đối xứng với đoạn thẳng AC qua đường thẳng d.
Cho tam giác ABC có AB < AC, gọi d là đường trung trực của BC. Vẽ K đối xứng với A qua d.
a) Tìm đoạn thẳng đối xứng với đoạn thẳng AB qua đường thẳng d; tìm đoạn thẳng đối xứng với đoạn thẳng AC qua đường thẳng d.
Xem đáp án »
13/07/2024
221
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
10 Bài tập Nhận biết hai hình đồng dạng, hai hình đồng dạng phối cảnh (có lời giải)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
Đề kiểm tra Cuối kì 2 Toán 8 CTST có đáp án (Đề 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận