Cho tam giác ABD. Vẽ điểm C đối xứng với A qua BD. Vẽ các đường phân giác ngoài tại các đỉnh A, B, C, D của tứ giác ABCD chúng cắt nhau tạo thành tứ giác EFGH.
a) Xác định dạng của tứ giác EFGH;
Cho tam giác ABD. Vẽ điểm C đối xứng với A qua BD. Vẽ các đường phân giác ngoài tại các đỉnh A, B, C, D của tứ giác ABCD chúng cắt nhau tạo thành tứ giác EFGH.
a) Xác định dạng của tứ giác EFGH;
Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 7: Đối xứng trục có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
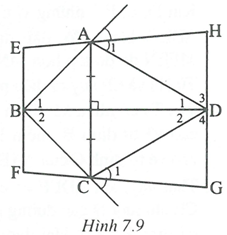
a) Vì C đối xứng với A qua BD nên đối xứng với qua BD.
Do đó , suy ra: ; và .
Ta có BD và BE là các tia phân giác trong và ngoài tại đỉnh B nên .
Chứng minh tương tự, ta được: .
Suy ra EF // HG => Tứ giác EFGH là hình thang.
Ta có (cùng phụ với hai góc bằng nhau).
(một nửa của hai góc bằng nhau).
Suy ra
Hình thang EFGH có hai góc kề một đáy bằng nhau nên là hình thang cân.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
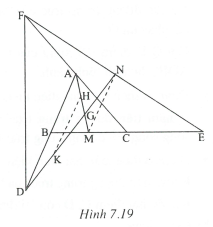
Vẽ đường trung tuyến AM của tam giác ABC và đường trung tuyến DN của tam giác DEF. Gọi G là giao điểm của hai đường trung tuyến này. Gọi H và K lần lượt là trung điểm của GA và GD.
Xét có AN là đường trung bình => AN // CE và do đó AN // BM và AN = BM dẫn tới ANMB là hình bình hành =>MN // AB và .
Mặt khác, HK là đường trung bình của nên HK // AD và .
Từ đó MN // HK và MN = HK.
Suy ra MNHK là hình bình hành, hai đường chéo HM và NK cắt nhau tại G nên G là trung điểm của mỗi đường.
Do đó GM = GH = HA => G là trọng tâm của .
GN = GK = KD => G là trọng tâm của .
Vậy và có cùng một trọng tâm.
Lời giải
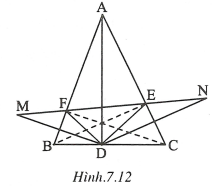
Vẽ điểm M đối xứng với D qua AB và vẽ điểm N đối xứng với D qua AC. Khi đó .
Chu vi
Chu vi nhỏ nhất khi độ dài đường gấp khúc MFEN ngắn nhất. Muốn vậy bốn điểm M, F, E, N phải thẳng hàng theo thứ tự đó.
Do đó ta phải tìm điểm D trên BC sao cho MN nhỏ nhất.
Theo kết quả bài 7.2, để MN nhỏ nhất thì D là hình chiếu của A trên BC. Khi đó E và F lần lượt là giao điểm của MN với AC và AB (h.7.12).
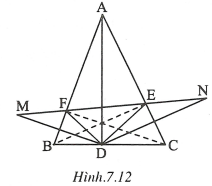
Ta chứng minh với cách xác định D, E, F như vậy thì chu vi nhỏ nhất.
Thật vậy, khi thì chu vi bằng MN và MN nhỏ nhất. (1)
Khi D, E, F ở những vị trí khác thì chu vi bằng độ dài đường gấp khúc MFEN do đó lớn hơn MN. (2)
Chú ý: Ta có nhận xét điểm E là chân đường cao vẽ từ đỉnh B, điểm F là chân đường cao vẽ từ đỉnh C của .
Thật vậy, xét có các đường BF và CE lần lượt là các đường phân giác ngoài tại đỉnh F và E. Hai đường thẳng này cắt nhau tại A nên tia DA là tia phân giác của góc EDF.
Ta có: nên DC là tia phân giác ngoài tại đỉnh D của .
Mặt khác, EC là đường phân giác ngoài tại đỉnh E.
Điểm C là giao điểm của hai đường phân giác ngoài nên FC là đường phân giác trong. Kết hợp với FB là đường phân giác, suy ra hay .
Chứng minh tương tự, ta được .
Như vậy ba điểm D, E, F có thể xác định bởi chân của ba đường cao của tam giác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập