Cho tam giác ABC. Vẽ điểm D đối xứng với A qua điểm B. Vẽ điểm E đối xứng với B qua C. Vẽ điểm F đối xứng với C qua A. Chứng minh rằng tam giác ABC và tam giác DEF có cùng một trọng tâm.
Cho tam giác ABC. Vẽ điểm D đối xứng với A qua điểm B. Vẽ điểm E đối xứng với B qua C. Vẽ điểm F đối xứng với C qua A. Chứng minh rằng tam giác ABC và tam giác DEF có cùng một trọng tâm.
Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 7: Đối xứng trục có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
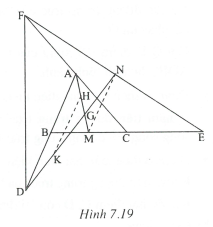
Vẽ đường trung tuyến AM của tam giác ABC và đường trung tuyến DN của tam giác DEF. Gọi G là giao điểm của hai đường trung tuyến này. Gọi H và K lần lượt là trung điểm của GA và GD.
Xét có AN là đường trung bình => AN // CE và do đó AN // BM và AN = BM dẫn tới ANMB là hình bình hành =>MN // AB và .
Mặt khác, HK là đường trung bình của nên HK // AD và .
Từ đó MN // HK và MN = HK.
Suy ra MNHK là hình bình hành, hai đường chéo HM và NK cắt nhau tại G nên G là trung điểm của mỗi đường.
Do đó GM = GH = HA => G là trọng tâm của .
GN = GK = KD => G là trọng tâm của .
Vậy và có cùng một trọng tâm.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
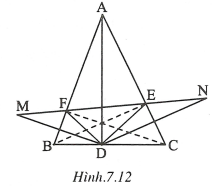
Vẽ điểm M đối xứng với D qua AB và vẽ điểm N đối xứng với D qua AC. Khi đó .
Chu vi
Chu vi nhỏ nhất khi độ dài đường gấp khúc MFEN ngắn nhất. Muốn vậy bốn điểm M, F, E, N phải thẳng hàng theo thứ tự đó.
Do đó ta phải tìm điểm D trên BC sao cho MN nhỏ nhất.
Theo kết quả bài 7.2, để MN nhỏ nhất thì D là hình chiếu của A trên BC. Khi đó E và F lần lượt là giao điểm của MN với AC và AB (h.7.12).
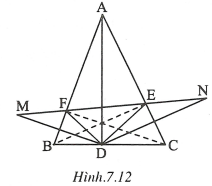
Ta chứng minh với cách xác định D, E, F như vậy thì chu vi nhỏ nhất.
Thật vậy, khi thì chu vi bằng MN và MN nhỏ nhất. (1)
Khi D, E, F ở những vị trí khác thì chu vi bằng độ dài đường gấp khúc MFEN do đó lớn hơn MN. (2)
Chú ý: Ta có nhận xét điểm E là chân đường cao vẽ từ đỉnh B, điểm F là chân đường cao vẽ từ đỉnh C của .
Thật vậy, xét có các đường BF và CE lần lượt là các đường phân giác ngoài tại đỉnh F và E. Hai đường thẳng này cắt nhau tại A nên tia DA là tia phân giác của góc EDF.
Ta có: nên DC là tia phân giác ngoài tại đỉnh D của .
Mặt khác, EC là đường phân giác ngoài tại đỉnh E.
Điểm C là giao điểm của hai đường phân giác ngoài nên FC là đường phân giác trong. Kết hợp với FB là đường phân giác, suy ra hay .
Chứng minh tương tự, ta được .
Như vậy ba điểm D, E, F có thể xác định bởi chân của ba đường cao của tam giác.
Lời giải
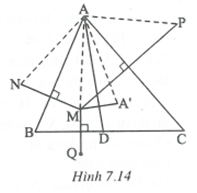
a)
- AN đối xứng với AM qua AB
=> AN = AM và . (1)
- AP đối xứng với AM qua AC
=> AP = AM và . (2)
·- AA' đối xứng với AM qua AD nên .
Mặt khác, nên (3)
Từ (1) và (3) suy ra .
Ta có .
Chứng minh tương tự, ta được: , suy ra: .
cân tại A có AA' là đường phân giác nên AA' cũng là đường trung trực của NP 
N và P đối xứng qua AA'.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập