Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác. M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB.
a) Chứng minh tứ giác MNPQ là hình bình hành.
Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác. M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB.
a) Chứng minh tứ giác MNPQ là hình bình hành.
Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 11: Hình chữ nhật có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
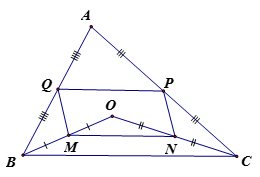
a) Ta có:
PQ là đường trung bình của tam giác ABC (1)
MN là đường trung bình của tam giác OBC (2)
Từ (1) và (2) suy ra
là hình bình hành.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
b) Để MNPQ là hình chữ nhật thì cần
Mà
Hơn nữa: QM // AO nên .
Vậy để MNPQ là hình chữ nhật là O nằm trên đường cao xuất phát từ đỉnh A của .
Lời giải
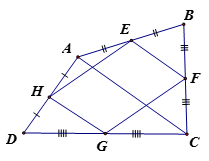
Ta có: là đường trung bình của và (1)
Ta có: là đường trung bình của và (2)
Từ (1), (2) suy ra EF // HG và EF = HG
Vậy EFGH là hình bình hành (3)
Để EFGH là hình chữ nhật thì .
Nhắn tin Zalo