Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 15: Hình vuông có đáp án !!
Quảng cáo
Trả lời:
b) Giả sử các đoạn thẳng DM, AN, BP, CQ giao nhau tạo thành tứ giác EFGH.
MB // DP và MB = DP => là hình bình hành.
Suy ra BP // DM => ANBP.
Tương tự ta cũng có .
Như vậy tứ giác EFGH có .
* Ta chứng minh EF = EH :
Dễ thấy EM là đường trung bình trong tam giác ABF, E là trung điểm của AF.
Tương tự H là trung điểm của DE.
Xét hai tam giác ABF và DAE vuông tại F là E, có:
AB = DA ; (vì ).
Suy ra
Từ đó ta có EF = EH. Vậy EFGH là hình vuông.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
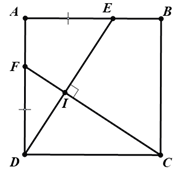
Gọi I là giao điểm của DE và CF.
Xét hai tam giác ADE và DCF có:
AD = DC (vì ABCD là hình vuông).
.
AE = DF (theo giả thiết)
Vậy , khi đó ta có:
DE = CF và .
Mặt khác , suy ra .
Vậy .
Lời giải
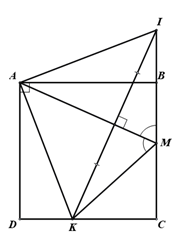
MA là phân giác góc BMK nên MA là trục đối xứng của hai đường thẳng MK và MB.
Gọi I là điểm đối xứng của K qua MA, suy ra I thuộc đường thẳng BC.
Ta có , .
Hai tam giác vuông ABI và ADK có hai cạnh bằng nhau nên .
Từ đó ta có .
.
Vậy ta có: .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.