✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

24/10/2022 1,067

Cho tam giác nhọn ABC .Từ một điểm I nằm trong tam giác ta kẻ IM ^ BC, IN ^ AC , IK ^AB . Đặt AK =x ; BM = y ; CN = z.Tìm vị trí của I sao cho tổng x² +y² +z²nhỏ nhất.

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 9 Chủ đề 7: Cực trị hình học có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

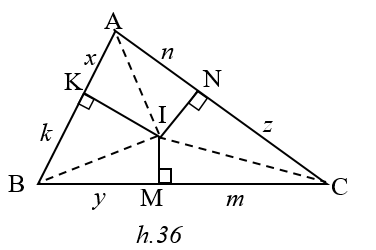
Media VietJack

Đặt BK = k , CM = m , AN = n ,

BC = a , AC = b , AB = c .

x² +y² +z² =

=(IA² - IK² ) + (IB² - IM² ) + (IC² - IN² )

= (IA² - IN² ) + (IB² - IK² ) + (IC² - IM² ) = n² + k² + m²

Þ 2(x² +y² +z² ) = x² +y² +z² + n² + k² + m²

= ( x²+ k² )+( y²+ m² )+( z²+ n² )

x²+ k² ≥ $\frac{{(x + k)}^{2}}{2} = \frac{A B^{2}}{2} = \frac{c^{2}}{2}$ y²+ m² ≥ $\frac{{(y + m)}^{2}}{2} = \frac{B C^{2}}{2} = \frac{a^{2}}{2}$

z²+ n² ≥ $\frac{{(z + n)}^{2}}{2} = \frac{A C^{2}}{2} = \frac{b^{2}}{2}$

Þ x² +y² +z² ≥ $\frac{a^{2} + b^{2} + c^{2}}{4}$ .

min(x² +y² +z² ) = $\frac{a^{2} + b^{2} + c^{2}}{4}$ Û x = k , y = m , z = n.

Û I là giao điểm của các đường trung trực của DABC.

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình vuông ABCD cạnh a .Vẽ cung BD tâm A bán kính a (nằm trong hình vuông ) .một tiếp tuyến bất kỳ với cung đó cắt BC, CD theo thứ tự ở M và N. Tính độ dài nhỏ nhất của MN.

Xem đáp án

Lời giải

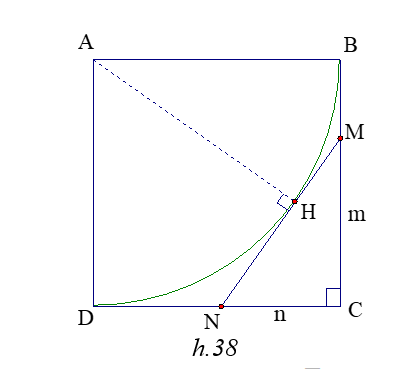
Media VietJack

Đặt CM = m , CN = n , MN = x

m + n + x = 2CD = 2a và m² +n² = x²

Do đó : x²= m² +n² ≥

$\Rightarrow$ 2x² ≥ ( 2a - x)² Þ ≥ 2a - x

$\Rightarrow$ x ≥

$\Rightarrow$ min MN =2a Û m = n . Khi đó tiếp tuyến MN // BD , AM là tia phân giác của

$\Rightarrow$ AN là phân giác của

Câu 2

Cho DABC nội tiếp đường tròn (O) D là điểm bất kỳ thuộc cung BC không chứa A và không trùng với B,C. Gọi H,I,K theo thứ tự là chân các đường vuông góc kẻ từ D đến các đường thẳng BC , AC, AB . Đặt BC = a , AC = b ,AB = c, DH = x , DI = y , DK = z . Chứng minh rằng : $\frac{b}{y} + \frac{c}{z} = \frac{a}{x}$

Xem đáp án

Lời giải

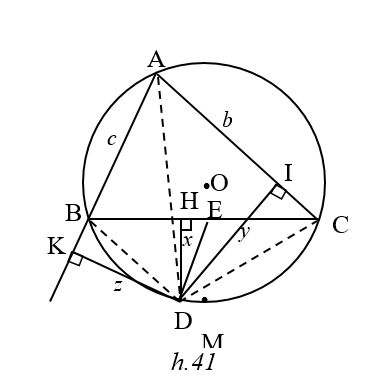
Media VietJack

Lấy E trên BC sao cho

DCDE đồng dạng với D ADB

Þ $\frac{D H}{D K} = \frac{C E}{A B} \Rightarrow \frac{x}{z} = \frac{C E}{c} \Rightarrow \frac{c}{z} = \frac{C E}{x}$

Tương tự DBDE đồng dạng với D ADC

Þ $\frac{D H}{D I} = \frac{B E}{A C} \Rightarrow \frac{x}{y} = \frac{B E}{b} \Rightarrow \frac{b}{y} = \frac{B E}{x}$

Þ $\frac{b}{y} + \frac{c}{z} = \frac{B E + C E}{x} = \frac{a}{x}$

Câu 3

Cho D ABC vuông tại A . Từ một điểm I nằm trong tam giác ta kẻ IM ^ BC, IN ^ AC , IK ^AB . Tìm vị trí của I sao cho tổng IM² +IN² +IK² nhỏ nhất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho đường tròn (O;R) . Trong đường tròn (O) vẽ hai đường tròn (O₁) và (O₂) tiếp xúc ngoài nhau và tiếp xúc trong với (O) trong đó bán kính đường tròn (O₂) gấp đôi bán kính đường tròn (O₁). Tìm giá trị nhỏ nhất của diện tích phần hình tròn (O) nằm ngoài các hình tròn (O₁) và(O₂)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho DABC nhọn , điểm M di chuyển trên cạnh BC .Gọi P ,Q là hình chiếu của M trên AB , AC . Xác định vị trí của điểm M để PQ có độ dài nhỏ nhất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho nửa đường tròn có đường kính AB = 10 cm .Một dây CD có độ dài 6cm có hai đầu di chuyển trên nửa đường tròn . Gọi E và F theo thứ tự là hình chiếu của A và B trên CD. Tính diện tích lớn nhất của tứ giác ABFE.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho đường tròn (O;R) đường kính BC , A là một điểm di động trên đường tròn . Vẽ tam giác đều ABM có A và M nằm cùng phía đối với BC . Gọi H là chân đường vuông góc kẻ từ C xuống MB. Gọi D, E , F, G theo thứ tự là trung điểm của OC, CM, MH, OH . Xác định vị trí của điểm A để diện tích tứ giác DEFG đạt giá trị lớn nhất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »