Thi Online Trắc nghiệm Toán 7 KNTT Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song có đáp án
Trắc nghiệm Toán 7 KNTT Dạng 1. Vận dụng tiên đề Euclid về hai đường thẳng song song và chứng minh ba điểm thẳng hàng có đáp án
-
315 lượt thi
-
12 câu hỏi
-
30 phút
Câu 1:
Cho AB // CD. Trên tia đối của tia BA lấy điểm E. Chứng minh BE // CD.
Cho AB // CD. Trên tia đối của tia BA lấy điểm E. Chứng minh BE // CD.
Hướng dẫn giải:
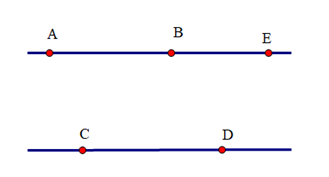
Ta có hai đường thẳng AB và CD song song với nhau.
Mà E nằm trên tia đối của tia BA.
Theo tiên đề Euclid ta có: Qua B chỉ kẻ được duy nhất một đường thẳng song song với CD.
Suy ra BE song song với CD.
Câu 2:
Cho MN // PQ; NO // PQ. Chứng minh ba điểm M, N, O thẳng hàng.
Hướng dẫn giải:
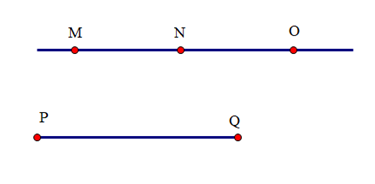
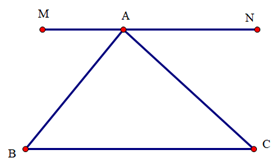
Theo tiên đề Euclid: chỉ có một đường thẳng đi qua N và song song với PQ.
Mà hai đường thẳng MN và NO đều đi qua N và song song với PQ.
Suy ra hai đường thẳng MN và NO trùng nhau.
Do đó ba điểm M, N, O thẳng hàng.
Vậy ba điểm M, N, O thẳng hàng.
Câu 3:
Tiên đề Euclid được phát biểu là:
Hướng dẫn giải:
Đáp án đúng là: A
Tiên đề Euclid được phát biểu là: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Câu 4:
Phát biểu nào sau đây diễn đạt đúng nội dung tiên đề Euclid?
Hướng dẫn giải:
Đáp án đúng là: A
Phát biểu diễn đạt đúng nội dung tiên đề Euclid là: Cho điểm M nằm ngoài đường thẳng a, đường thẳng đi qua M và song song với a là duy nhất. Do đó A đúng.
Phương án B sai vì có vô số đường thẳng song song với đường thẳng cho trước.
Phương án C sai vì qua điểm M ở ngoài đường thẳng a, chỉ có duy nhất một đường thẳng song song với a.
Vậy ta chọn A.
Câu 5:
Cho hình vẽ sau:
Biết AB // CD. Phát biểu đúng là:
Cho hình vẽ sau:
Biết AB // CD. Phát biểu đúng là:
Hướng dẫn giải:
Đáp án đúng là: B
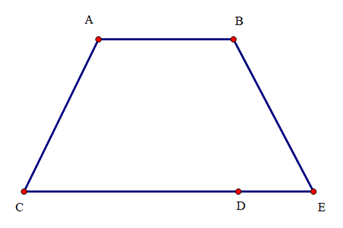
Ta có AB // CD.
Mà CD và CE cùng đi qua điểm C nên theo tiên đề Euclid chỉ có một đường thẳng qua C và song song với AB.
Suy ra AB // CE.
Bài thi liên quan
Có thể bạn quan tâm
Các bài thi hot trong chương
Đánh giá trung bình
0%
0%
0%
0%
0%