Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
A. 17,5
B. 18
C. 18,5
D. 19
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Xét Δ ABD và Δ BDC có:
⇒ AB/BD = AD/BC = BD/DC
hay 12,5/x = x/28,5 ⇒ x2 = 1425/4 ⇔ x ≈ 18,87
Chọn đáp án D.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải:
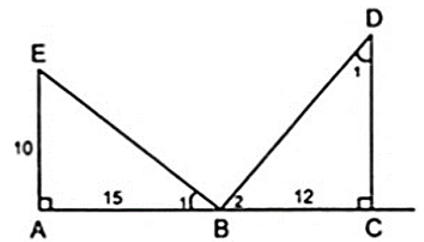
a) Ta có:
BA/BD = AD/BC = BD/CD = 1/2 ⇒ Δ BAD ∼ Δ DBC ( c - c - c )
b) Ta có: Δ BAD ∼ Δ DBC
⇒ ABDˆ = BDCˆ nên AB//CD
⇒ ABCD là hình thang.
Lời giải
Hướng dẫn giải:
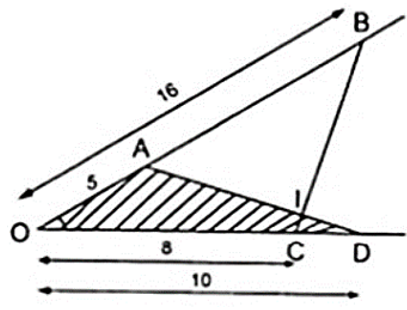
a) Xét Δ OCB và Δ OAD có
⇒ Δ OCB ∼ Δ OAD ( c - g - c )
b) Ta có: Δ OCB ∼ Δ OAD
⇒ ADOˆ = CBOˆ hay IDCˆ = IBAˆ
Mà CIDˆ = AIBˆ (vì đối đỉnh) ⇒ ICDˆ = IAB
Câu 3
A. Δ ABC, Δ DEF;AB/DE = AC/DF;Bˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
B. Δ ABC, Δ DEF;AB/DE = AC/DF;Cˆ = Fˆ ⇒ Δ ABC ∼ Δ DEF
C. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Dˆ ⇒ Δ ABC ∼ Δ DEF
D. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Δ ABC ∼ Δ DEF
B. ABCˆ = EFDˆ
C. ACBˆ = ADFˆ
D. ACBˆ = DEFˆ
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Δ RSK ∼ Δ PQM
B. Δ RSK ∼ Δ MPQ
C. Δ RSK ∼ Δ QPM
D. Δ RSK ∼ Δ QMP
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo