Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ . Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
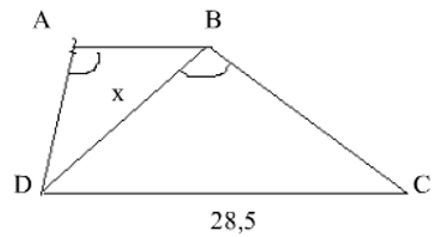
Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ . Tính độ dài đoạn BD gần nhất bằng bao nhiêu?

Quảng cáo
Trả lời:
Hướng dẫn giải:
Xét Δ ABD và Δ BDC có:
⇒ AB/BD = AD/BC = BD/DC hay 12,5/x = x/28,5 ⇒ x2 = 1425/4 ⇔ x ≈ 18,87
Chọn đáp án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải:
Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
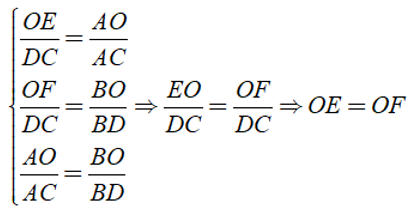
Điều phải chứng minh.
Lời giải
Hướng dẫn giải:
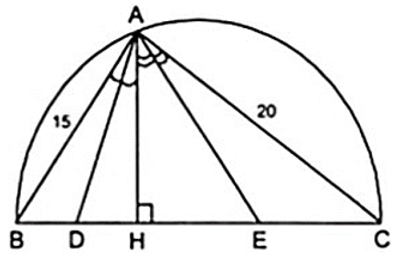
Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A, ta được:
B C2 = A C2 + A B2 ⇒ B C2 = 152 + 202
⇔ B C2 = 252 ⇔ BC = 25( cm )
Đặt BD = x ⇒ DC = 25 - x
Áp dụng định lý Py 0 ta – go vào hai tam giác vuông AHB và AHC, ta được:
Trừ theo vế các đẳng thức ( 1 ) và ( 2 ) ta được:
152 - x2 - 202 + ( 25 - x )2 = 0 ⇔ 50x = 450 ⇔ x = 9( cm )
Nên HC = 25 - 9 = 16( cm )
Thay x = 9 vào đẳng thức ( 1 ) ta có: H A2 = 152 - 92 = 122 ⇔ HA = 12( cm )
Áp dụng tính chất đường phân giác AD vào tam giác AHB, ta được:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
Áp dụng tính chất đường chất đường phân giác AE của tam giác ACH, ta được:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
