Cho tam giác ABC có A^=120° , AD là đường phân giác. Chứng minh rằng: 1AB+1AC=1AD.

Kẻ DE // AB, ta có: D1^=A1^=60°; A2^=60° nên tam giác ADE đều. Suy ra AD = AE = DE. Áp dụng hệ quả định lý Ta-lét:DEAB=CEAC hay ADAB=CEAC. Mặt khác ADAC=AEAC nên ADAB+ADAC=CEAC+AEAC=ACAC=1. Suy ra 1AB+1AC=1AD. Nhận xét. Những bài toán chứng minh đẳng thức có nghịch đảo độ dài đoạn thẳng, bạn nên biến đổi và chứng minh hệ thức tương đương có tỉ số của hai đoạn thẳng.

Câu hỏi:

19/08/2025 16,538

Cho tam giác ABC có $\hat{A} = 120 °$ , AD là đường phân giác. Chứng minh rằng: $\frac{1}{A B} + \frac{1}{A C} = \frac{1}{A D} .$

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 2: Định lí đảo và hệ quả của Định lí Ta-lét có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

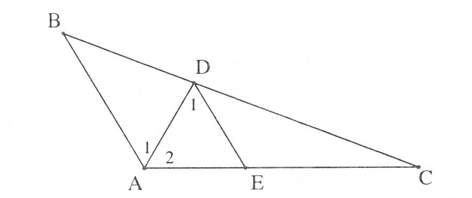
Media VietJack

Kẻ DE // AB, ta có:

$\hat{D_{1}} = \hat{A_{1}} = 60 °; \hat{A_{2}} = 60 °$ nên tam giác ADE đều. Suy ra AD = AE = DE.

Áp dụng hệ quả định lý Ta-lét: $\frac{D E}{A B} = \frac{C E}{A C}$ hay $\frac{A D}{A B} = \frac{C E}{A C} .$

Mặt khác $\frac{A D}{A C} = \frac{A E}{A C}$ nên $\frac{A D}{A B} + \frac{A D}{A C} = \frac{C E}{A C} + \frac{A E}{A C} = \frac{A C}{A C} = 1.$

Suy ra $\frac{1}{A B} + \frac{1}{A C} = \frac{1}{A D} .$

Nhận xét. Những bài toán chứng minh đẳng thức có nghịch đảo độ dài đoạn thẳng, bạn nên biến đổi và chứng minh hệ thức tương đương có tỉ số của hai đoạn thẳng.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

Hà NBS Nguyễn Thị

cảm ơn nhé ! làm rất hay

1 năm trước
Trả lời

Xem thêm ...

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng:

$\frac{A B}{A M} + \frac{A C}{A N} = 3;$

Xem đáp án

Lời giải

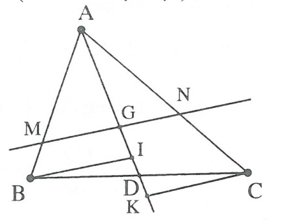
* Tìm cách giải. Để tạo ra tỉ số $\frac{A B}{A M}; \frac{A C}{A N}$ chúng ta cần vận dụng định lý Ta-let, mà hình vẽ chưa có yếu tố song song do vậy chúng ta cần kẻ thêm yếu tố song song. Kẻ đường thẳng song song với MN từ B và C vừa khai thác được yếu tố trọng tâm, vừa tạo ra được tỉ số yêu cầu.

* Trình bày lời giải

Trường hợp 1. Nếu MN // BC, thì lời giải giản đơn (dành cho bạn đọc).

Trường hợp 2. Xét MN không song song với BC.

Gọi giao điểm của AG và BC là D $\Rightarrow B D = C D .$

Kẻ BI // CK // MN $(I, K \in A D)$

Xét $Δ B D I$ và $Δ C D K$ có $B D = C D; \hat{I B D} = \hat{K C D}; \hat{I D B} = \hat{K D C}$ nên $Δ B D I = Δ C D K (g . c g)$

$\Rightarrow D I = D K .$

Áp dụng định lý Ta-lét, ta có $\frac{A B}{A M} = \frac{A I}{A G}$ (vì MG // BI);

$\frac{A C}{A N} = \frac{A K}{A G}$ (vì GN // CK).

Suy ra $\frac{A B}{A M} + \frac{A C}{A N} = \frac{2. A D}{A G} = 3$ (1) (vì $A D = \frac{3}{2} . A G$ ).

Câu 2

Cho tam giác ABC có AD là đường trung tuyến. Gọi M là điểm tùy ý thuộc khoảng BD. Lấy E thuộc AB và F thuộc AC sao cho ME // AC; MF // AB. Gọi H là giao điểm MF và AD. Đường thẳng qua B song song với EH cắt MF tại K. Đường thẳng AK cắt BC tại I. Tính tỉ số $\frac{I B}{I D}$ ?

Xem đáp án

Lời giải

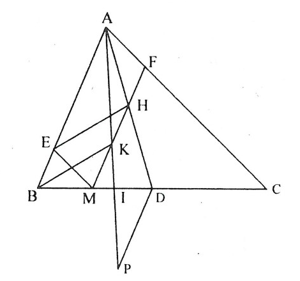
Media VietJack

Qua D kẻ đường thẳng song song với AB, cắt tia AI tại P. Áp dụng định lý Ta-let, cho các đoạn thẳng song song ta có:

$DP//AB \Rightarrow \frac{I B}{I D} = \frac{A B}{D P} = \frac{A B}{H K} . \frac{H K}{D P}$ (1).

$ME//AC \Rightarrow \frac{A B}{H K} = \frac{A B}{B E} = \frac{B C}{B M}$ (2).

và $MH//AB \Rightarrow \frac{H K}{D P} = \frac{A H}{A D} = \frac{B M}{B D}$ (3).

Từ (1), (2) và (3) suy ra:

$\frac{I B}{I D} = \frac{B C}{B M} . \frac{B M}{B D} = \frac{B C}{B D} = 2$ . Vậy $\frac{I B}{I D} = 2.$

Câu 3

Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng: $\frac{B M}{A M} + \frac{C N}{A N} = 1.$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC nhọn có AH là đường cao. Trên AH, AB, AC lần lượt lấy điểm D, E, F sao cho $\hat{E D C} = \hat{F D B} = 90 °$ . Chứng minh rằng: $EF//BC$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO; AO. Lấy F trên cạnh AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng: $\frac{B A}{B F} + \frac{B C}{B E} = 4;$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO; AO. Lấy F trên cạnh AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng: $B E + A K \geq B C .$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Cho tam giác ABC có $\hat{A} = 120 °$ , AD là đường phân giác. Chứng minh rằng: $\frac{1}{A B} + \frac{1}{A C} = \frac{1}{A D} .$

Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng:

$\frac{A B}{A M} + \frac{A C}{A N} = 3;$

Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng: $\frac{B M}{A M} + \frac{C N}{A N} = 1.$

Cho tam giác ABC nhọn có AH là đường cao. Trên AH, AB, AC lần lượt lấy điểm D, E, F sao cho $\hat{E D C} = \hat{F D B} = 90 °$ . Chứng minh rằng: $EF//BC$ .

Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO; AO. Lấy F trên cạnh AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng: $\frac{B A}{B F} + \frac{B C}{B E} = 4;$

Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO; AO. Lấy F trên cạnh AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng: $B E + A K \geq B C .$