Cho tam giác ABC, cạnh BC cố định. Vẽ ra ngoài tam giác này các tam giác ABM vuông cân tại B, tam giác CAN vuông cân tại C. Chứng minh rằng khi A di động trên một nửa mặt phẳng bờ BC thì đường thẳng MN luôn đi qua một điểm cố định.
Cho tam giác ABC, cạnh BC cố định. Vẽ ra ngoài tam giác này các tam giác ABM vuông cân tại B, tam giác CAN vuông cân tại C. Chứng minh rằng khi A di động trên một nửa mặt phẳng bờ BC thì đường thẳng MN luôn đi qua một điểm cố định.
Quảng cáo
Trả lời:

Gọi O là trung điểm của MN.
Vẽ và
Ta có:
(cạnh huyền – góc nhọn)
=> MD = BH và BD = AH
Tương tự,
=> NE = CH và CE = AH (2)
Từ (1) và (2) suy ra BD = CE (=AH).
Dễ thấy OF là đường trung bình của hình thang MDEN
(không đổi).
Ta có: .
Vậy O nằm trên đường trung trực của BC và cách BC một khoảng không đổi là . Do đó O là một điểm cố định.
Suy ra MN đi qua một điểm cố định là điểm O.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
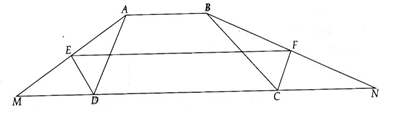
a) Gọi M và N lần lượt là giao điểm của AE, BF với CD.
Ta có: ngoài, ngoài.
Mà ngoài + ngoài = 1800 (do AB//CD)
, tức là tam giác ADE vuông tại E.
Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.
Chứng minh tương tự, ta được F là trung điểm của BN.
Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM
Lời giải
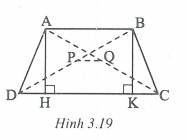
a) Vẽ ta được AH // BK và AB // HK
Ta có:
Theo ví dụ 4 thì đoạn thẳng PQ nối trung điểm của hai đường chéo bằng nửa hiệu hai đáy. Vậy HD = PQ
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.