khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 8
  3. Toán

Câu hỏi:

19/08/2025 453 Lưu

b)  Ba điểm B, I, D thẳng hàng.

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 15: Hình vuông có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

b) 

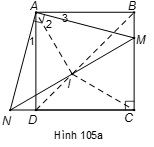
b)  Ba điểm B, I, D  thẳng hàng. (ảnh 1)

Cách 1 (hình 105a): Nối IA, IC thì IA và IC lần lượt là các đường trung tuyến ứng với cạnh huyền của hai tam giác vuông AMN, CMN.

Áp dụng tính chất đường trung tuyến ứng với cạnh huyền vào hai tam giác vuông trên và định nghĩa hình vuông ta được IA=IC=12MNBA=BC.

Điều này chứng tỏ hai điểm B và I cách đều hai điểm A và C nên BI là đường trung trực của đoạn AC. Mặt khác theo tính chất về đường chéo của hình vuông thì BD là trung trực của AC mà đoạn AC thì chỉ có một đường trung trực nên BI trùng với BD hay B, I, D thẳng hàng.

Cách 2 (hình 105b):

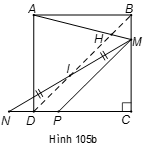
b)  Ba điểm B, I, D  thẳng hàng. (ảnh 2)

Qua M kẻ MP // BD  (1) (điểm P∈DC) suy ra DI // MP (2).

Lại có NI = MI (3) theo giả thiết. Từ (2) và (3) suy ra ND = DP (4)
theo định lí đường trung bình.

Từ (3) và (4) ta có DI là đường trung bình của tam giác NMP.

Áp dụng định lí đường trung bình vào tam giác NMP ta được DI // MP (5).
Từ (1) và (5) suy ra B, I, D thẳng hàng, vì từ điểm I ở ngoài đường thẳng MP chỉ kẻ được một đường thẳng song song với MP.

Cách 3: Qua M kẻ MH // ND (1) (điểm H∈BD) thì D1^=H1^ (2) do đồng vị.

Mà BD là đường chéo của hình vuông ABCD nên BD là đường phân giác của hai góc vuông B và D do đó D1^=H1^=450 (3).

Từ (2) và (3) ta có BM = MH (4) vì trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau.

Kết hợp (1) với (4) ta được tứ giác NHMD có hai cạnh đối song song và bằng nhau nên nó là hình bình hành.

Áp dụng tính chất về đường chéo vào hình bình hành NHMD, ta được đường chéo DH đi qua trung điểm I của đường chéo NM nên BD đi qua I.

Điều đó chứng tỏ B, I, D thẳng hàng.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, trên cạnh CD lấy điểm N sao cho BM = CN và AM⊥BN.

Lời giải

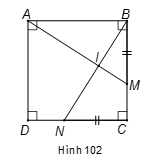
Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, trên cạnh CD lấy điểm N sao cho BM = CN và AM vuông BN (ảnh 1)

Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được:

      AB=BCA^=B^=900BM=CN

⇒ΔABM=ΔBCN (c.g.c), nên AM = BN.

Gọi I là giao diểm của AM và BN.

Áp dụng tính chất về góc vào tam giác vuông ABM và BCN kết quả của hai tam giác bằng nhau, ta được:

      A1^+M1^=900B1^=A1^⇒B1^+M1^=900                                               (1)

Áp dụng tính chất về góc vào tam giác BIM ta có B1^+M1^+I1^=1800     (2)

Từ (1) và (2) suy ra I^=1800−900=900 hay AM⊥BN.

Câu 2

Bổ đề về hình vuông

Cho hình vuông ABCD. Nếu các điểm M, N, P, Q lần lượt nằm trên các đường thẳng AB, BC, CD và DA thì

a) MP=NQ⇔MP⊥NQ.

Lời giải

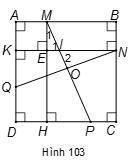
Cho hình vuông ABCD. Nếu các điểm M, N, P, Q lần lượt nằm trên các đường thẳng AB, BC, CD và DA thì . (ảnh 1)

Ta cần chứng minh bài toán đúng với các điểm M, N, P, Q nằm trên các cạnh AB, BC, CD, DA (các trường hợp còn lại chứng minh tương tự).

Gọi H, K lần lượt là chân các đường vuông góc kẻ từ M, N đến hai cạnh CD, DA và E, I, O thứ tự là giao điểm của MH với NK, MP với NQ.

Áp dụng định nghĩa vào hình vuông ABCD và tính chất góc đồng vị của KN // DC, ta được A^=B^=C^=E^=K^=N^=900.

Các tứ giác MBHC, KNCD và MBNE là các tứ giác có ba góc vuông nên chúng là các hình chữ nhật.

a)   MP=NQ⇒MP⊥NQ.

Áp dụng tính chất về cạnh và giả thiết vào hai hình chữ nhật MBCH, KNCD và hình vuông ABCD ta được:

      MH=BC,NK=CDBC=CD,MP=NQ⇒MH=MKMP=NQ⇒ΔMHP=ΔNKQ (trường hợp cạnh huyền, cạnh góc vuông).

Áp dụng tính chất về góc vào hai tam giác bằng nhau ở trên và tính chất của hai góc đối đỉnh ta có

M1^=N1^I1^=I2^⇒O^=E^=900 (vì hai tam giác, có hai cặp góc bằng nhau thì cặp góc thứ ba cũng bằng nhau).

Vậy MP vuông góc với NQ tại O.

Câu 3

Cho hình vuông ABCD cạnh a. Trên hai cạnh BC, BD lấy hai điểm M, N sao cho MAN^=450, trên tia đối của tia DC lấy điểm K sao cho DK = BM. Hãy tính:

a) Số đo góc KAN.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, qua A kẻ AN⊥AM (điểm N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh rằng:

a) AM = AN.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

b) Chu vi tam giác MCN theo a .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

b)  MP⊥NQ⇒MP=NQ.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập