Câu hỏi:

13/07/2024 1,439

Thống kê tại một trung tâm mua sắm gồm 46 cửa hàng, với 26 cửa hàng có bán quần áo, 16 cửa hàng có bán giày và 34 cửa hàng bán ít nhất một trong hai mặt hàng này. Hỏi:
Có bao nhiêu cửa hàng không bán cả hai loại hàng hóa trên?

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 10 Bài tập cuối chương 1 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

Ta biểu diễn bằng biểu đồ Ven như dưới đây:

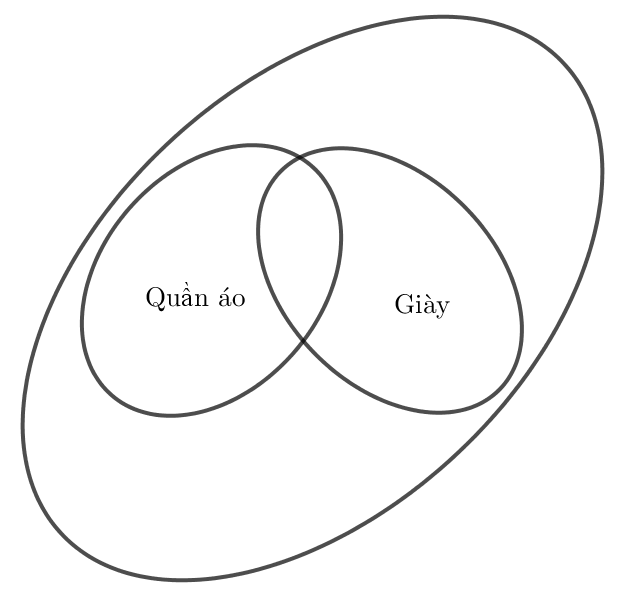
Những cửa hàng bán quần áo được đại diện bởi hình elip “Quần áo”.

Những cửa hàng bán giày được đại diện bởi hình elip “Giày”.

Phần giao của hình elip “Quần áo” và elip “Giày” là những cửa hàng bán cả quần áo và giày.

Hình elip lớn nhất đại diện cho tổng số cửa hàng tại trung tâm mua sắm, phần nằm bên ngoài 2 elip “Quần áo”, “Giày” và bên trong elip lớn đại diện cho những cửa hàng không bán cả quần áo và giày.

Số cửa hàng không bán hai mặt hàng trên bằng tổng số cửa hàng trong trung tâm mua sắm trừ đi số cửa hàng bán ít nhất một trong hai mặt hàng.

Do đó số cửa hàng không bán hai mặt hàng trên là 46 34 = 12 (cửa hàng).

Vậy có 12 cửa hàng không bán hai mặt hàng trên.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Lớp 10A có 40 học sinh, trong đó có 20 học sinh thích môn Ngữ văn, 18 học sinh thích môn Toán, 4 học sinh thích cả hai môn Ngữ văn và Toán. Hỏi có bao nhiêu học sinh không thích môn nào trong hai môn Ngữ văn và Toán?

Xem đáp án

Lời giải

Lời giải:

Trong 20 học sinh thích môn Ngữ Văn thì có 4 học sinh thích cả môn Ngữ văn và Toán.

Trong 18 học sinh thích môn Toán thì có 4 học sinh thích cả môn Ngữ văn và Toán.

Do đó số học sinh thích môn Ngữ văn hoặc Toán là: 20 + 18 4 = 34 (học sinh).

Số học sinh không thích môn nào trong hai môn Ngữ văn và Toán là:

40 34 = 6 (học sinh).

Vậy có 6 học sinh không thích môn nào trong hai môn Ngữ văn và Toán.

Câu 2

Hãy viết các tập hợp sau bằng cách liệt kê các phần tử của tập hợp.

A = {x $\in$ ℚ | (2x + 1)(x² + x $-$ 1)(2x² $-$ 3x + 1) = 0};

B = {x $\in$ ℕ | x² > 2 và x < 4}.

Xem đáp án

Lời giải

Lời giải:

Xét tập A = {x $\in$ ℚ | (2x + 1)(x² + x $-$ 1)(2x² $-$ 3x + 1) = 0}

(2x + 1)(x² + x $-$ 1)(2x² $-$ 3x + 1) = 0

Trường hợp 1.

2x + 1 = 0

$\Leftrightarrow$ 2x = 1

x = \[\frac{{ - 1}}{2} \in \mathbb{Q}\]

Trường hợp 2.

x² + x $-$ 1 = 0

$∆$ = 1² 4.(1) = 5 > 0.

Do đó phương trình có hai nghiệm phân biệt:

x₁ = \[\frac{{ - 1 - \sqrt 5 }}{2} \notin \mathbb{Q}\] (do \[ - 1 - \sqrt 5 \notin \mathbb{Q}\]);

x₂ = \[\frac{{ - 1 + \sqrt 5 }}{2} \notin \mathbb{Q}\] (do \[ - 1 + \sqrt 5 \notin \mathbb{Q}\]);

Trường hợp 3.

2x² $-$ 3x + 1 = 0

2x² - 2x - x + 1 = 0

2x(x - 1) (x 1) = 0

(x - 1)(2x - 1) = 0

\[ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\2{\rm{x}} - 1 = 0\end{array} \right.\]

\[ \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \mathbb{Q}\\x = \frac{1}{2} \in \mathbb{Q}\end{array} \right.\]

Vậy A = \[\left\{ {\frac{{ - 1}}{2};\frac{1}{2};1} \right\}.\]

Xét tập B = {x $\in$ ℕ | x² > 2 và x < 4}

Vì x $\in$ ℕ và x < 4 nên x {0; 1; 2; 3}.

Ta có 0² = 0 < 2; 1²= 1 < 2; 22</> = 4 > 2; 32 = 9 > 2.

Do đó B = {2; 3}.

Câu 3

Cho ba tập hợp sau:

E = {x $\in$ ℝ | f(x) = 0};

F = {x $\in$ ℝ | g(x) = 0};

H = {x $\in$ ℝ | f(x) . g(x) = 0};

Trong các mệnh đề sau, mệnh đề nào đúng?

A. H = E ∩ F.

B. H = E ∪ F.

C. H = E \ F.

D. H = F \ E.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Lớp 10A có 10 học sinh giỏi môn Toán, 15 học sinh giỏi môn Vật lí, 8 học sinh giỏi cả môn Toán và Vật lí. Số học sinh giỏi ít nhất một môn (Toán hoặc Vật lí) của lớp 10A là

A. 17.

B. 25.

C. 18.

D. 23.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hai tập hợp A = ( $- \infty$ ; -1] và B = (-2; 4]. Tìm mệnh đề sai.

A. A ∩ B = (-2; -1].

B. A \ B = ( $- \infty$ ; -2).

C. A ∪ B = ( $- \infty$ ; 4].

D. B \ A = (-1; 4].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hai tập hợp M = {x $\in$ ℤ | x² $-$ 3x $-$ 4 = 0} và N = {a; $-$ 1}. Với giá trị nào của a thì M = N?

A. a = 2.

B. a = 4.

C. a = 3.

D. a = $-$ 1 hoặc a = 4.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Thống kê tại một trung tâm mua sắm gồm 46 cửa hàng, với 26 cửa hàng có bán quần áo, 16 cửa hàng có bán giày và 34 cửa hàng bán ít nhất một trong hai mặt hàng này. Hỏi:
Có bao nhiêu cửa hàng chỉ bán một trong hai loại quần áo hoặc giày?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Thống kê tại một trung tâm mua sắm gồm 46 cửa hàng, với 26 cửa hàng có bán quần áo, 16 cửa hàng có bán giày và 34 cửa hàng bán ít nhất một trong hai mặt hàng này. Hỏi:Có bao nhiêu cửa hàng không bán cả hai loại hàng hóa trên?

Bình luận

Lớp 10A có 40 học sinh, trong đó có 20 học sinh thích môn Ngữ văn, 18 học sinh thích môn Toán, 4 học sinh thích cả hai môn Ngữ văn và Toán. Hỏi có bao nhiêu học sinh không thích môn nào trong hai môn Ngữ văn và Toán?

Hãy viết các tập hợp sau bằng cách liệt kê các phần tử của tập hợp. A = {x ∈ℚ | (2x + 1)(x2 + x -1)(2x2 -3x + 1) = 0}; B = {x ∈ℕ | x2 > 2 và x < 4}.

Cho ba tập hợp sau: E = {x ∈ ℝ | f(x) = 0}; F = {x ∈ℝ | g(x) = 0}; H = {x ∈ℝ | f(x) . g(x) = 0}; Trong các mệnh đề sau, mệnh đề nào đúng?

Lớp 10A có 10 học sinh giỏi môn Toán, 15 học sinh giỏi môn Vật lí, 8 học sinh giỏi cả môn Toán và Vật lí. Số học sinh giỏi ít nhất một môn (Toán hoặc Vật lí) của lớp 10A là

Cho hai tập hợp A = (-∞; -1] và B = (-2; 4]. Tìm mệnh đề sai.

Cho hai tập hợp M = {x∈ ℤ | x2 -3x -4 = 0} và N = {a; -1}. Với giá trị nào của a thì M = N?

Thống kê tại một trung tâm mua sắm gồm 46 cửa hàng, với 26 cửa hàng có bán quần áo, 16 cửa hàng có bán giày và 34 cửa hàng bán ít nhất một trong hai mặt hàng này. Hỏi:Có bao nhiêu cửa hàng chỉ bán một trong hai loại quần áo hoặc giày?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Thống kê tại một trung tâm mua sắm gồm 46 cửa hàng, với 26 cửa hàng có bán quần áo, 16 cửa hàng có bán giày và 34 cửa hàng bán ít nhất một trong hai mặt hàng này. Hỏi:
Có bao nhiêu cửa hàng không bán cả hai loại hàng hóa trên?

Hãy viết các tập hợp sau bằng cách liệt kê các phần tử của tập hợp.

A = {x $\in$ ℚ | (2x + 1)(x² + x $-$ 1)(2x² $-$ 3x + 1) = 0};

B = {x $\in$ ℕ | x² > 2 và x < 4}.

Cho ba tập hợp sau:

E = {x $\in$ ℝ | f(x) = 0};

F = {x $\in$ ℝ | g(x) = 0};

H = {x $\in$ ℝ | f(x) . g(x) = 0};

Trong các mệnh đề sau, mệnh đề nào đúng?

Cho hai tập hợp A = ( $- \infty$ ; -1] và B = (-2; 4]. Tìm mệnh đề sai.

Cho hai tập hợp M = {x $\in$ ℤ | x² $-$ 3x $-$ 4 = 0} và N = {a; $-$ 1}. Với giá trị nào của a thì M = N?