3 câu Trắc nghiệm Tam giác cân. Đường trung trực của đoạn thẳng có đáp án (Vận dụng)
22 người thi tuần này 4.0 2 K lượt thi 3 câu hỏi 30 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
24.5 K lượt thi
15 câu hỏi
5 câu Trắc nghiệm Tập hợp các số hữu tỉ có đáp án (Nhận biết)
6.7 K lượt thi
5 câu hỏi
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
1 K lượt thi
21 câu hỏi
5 câu Trắc nghiệm Toán 7 Bài 7: Tính chất đường trung trực của một đoạn thẳng có đáp án (Nhận biết)
4.5 K lượt thi
5 câu hỏi
4 câu Trắc nghiệm Toán 7 Bài 5: Tính chất tia phân giác của một góc có đáp án (Thông hiểu)
4.1 K lượt thi
4 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
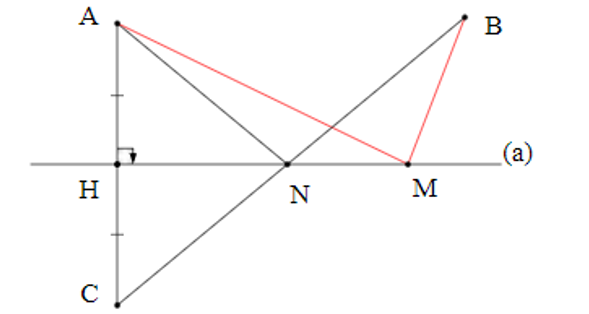
Câu 1
A. M trùng N;
B. M là điểm bất kì trên đường thẳng (a);
C. M trùng H;
D. Không có điểm M nào thỏa mãn yêu cầu bài toán.
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có (a) đi qua trung điểm H của đoạn thẳng AC và vuông góc với AC tại H.
Suy ra (a) là đường trung trực của đoạn thẳng AC.
Vì M ∈ (a) nên M cách đều A và C. Tức là, MA = MC.
Ta có MA + MB = MC + MB ≥ BC.
Vì vậy MA + MC nhỏ nhất khi và chỉ khi MA + MC = BC.
Tức là M là giao điểm của (a) và BC.
Khi đó M trùng N.
Vậy ta chọn phương án A.
Câu 2
A. P nằm trên đường trung trực của đoạn thẳng AB;
B. M nằm trên đường trung trực của đoạn thẳng AB;
C. N nằm trên đường trung trực của đoạn thẳng AB;
D. Ba điểm M, N, P không thẳng hàng.
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
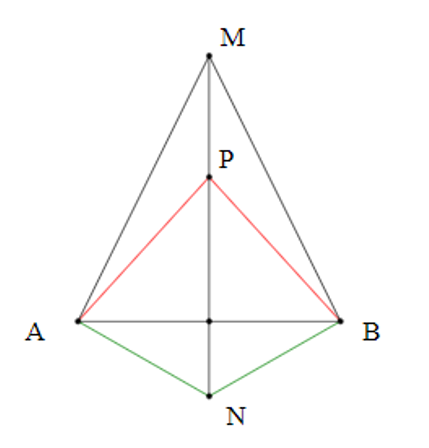
Ta có ∆MAB cân tại M.
Suy ra MA = MB.
Khi đó M nằm trên đường trung trực của đoạn thẳng AB.
Chứng minh tương tự, ta được N, P cũng nằm trên đường trung trực của đoạn thẳng AB.
Do đó ba điểm M, N, P thẳng hàng.
Vì vậy phương án A, B, C đúng, phương án D sai.
Vậy ta chọn phương án D.
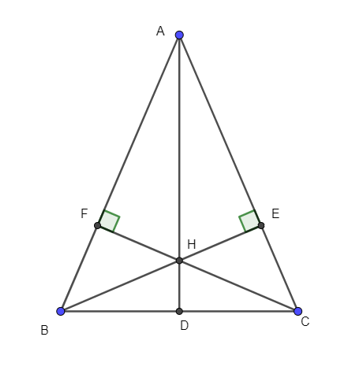
Câu 3
A. A, H, D thẳng hàng;
B. AH là tia phân giác của .
C. HD là đường trung trực của BC.
D. Cả A, B, C đều đúng.
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
+) Xét ∆ABE và ∆ACF, có:
AB = AC (tính chất đường trung trực của đoạn thẳng)
là góc chung
Do đó ∆ABE = ∆ACF (cạnh huyền – góc nhọn)
Suy ra AE = AF (hai cạnh tương ứng)
+) Xét ∆AEH và ∆AFH, có:
AH là cạnh chung.
AE = AF (chứng minh trên)
Do đó ∆AEH = ∆AFH (cạnh góc vuông – cạnh huyền)
Suy ra (cặp góc tương ứng) và EH = FH (cặp cạnh tương ứng)
Ta có nên AH là tia phân giác nên phát biểu B đúng.
+) Xét ∆BFH và ∆CEH, có:
HF = HE (chứng minh trên)
(hai góc đối đỉnh)
Do đó ∆BFH = ∆CEH (cạnh góc vuông – góc nhọn)
Suy ra HB = HC
Do đó H thuộc đường trung trực của BC.
Mặt khác ta có AB = AC nên A cũng thuộc trung trực của BC.
Suy ra AH là đường trung trực của BC nên AH đi qua điểm D khi đó A, H, D thẳng hàng hay ta cũng có HD là trung trực của BC. Do đó phát biểu A đúng và C đúng.
Vậy chọn đáp án D.
Nhắn tin Zalo
Hỏi bài tập