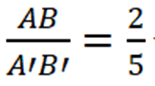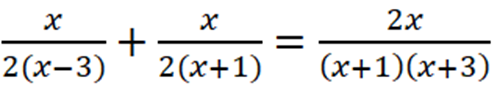✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

22/08/2022 215

Giải phương trình và bất phương trình sau :

$\frac{2 x}{x - 1} + \frac{3 (x + 1)}{x} = 5$

Xem lời giải

Câu hỏi trong đề: Trắc nghiệm chuyên đề Toán 8 Chủ đề 2: Kiểm tra học kì 2 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

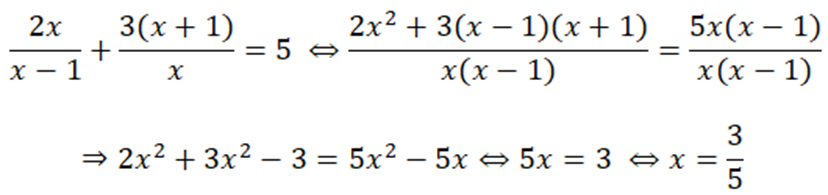
Giải phương trình và bất phương trình sau : 2x/x-1+3(x+1)/x=5 (ảnh 1)

thỏa mãn ĐKXD)

Tập nghiệm của (1): S = {3/5}

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC có ba góc nhọn, biết AB = 15cm, AC = 13cm và đường cao AH = 12cm. Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB.

a) Chứng minh rằng ΔAHN ∼ ΔACH

b) Tính độ dài BC

c) Chứng minh ΔAMN ∼ ΔACB

d) Tính MN

Xem đáp án

Lời giải

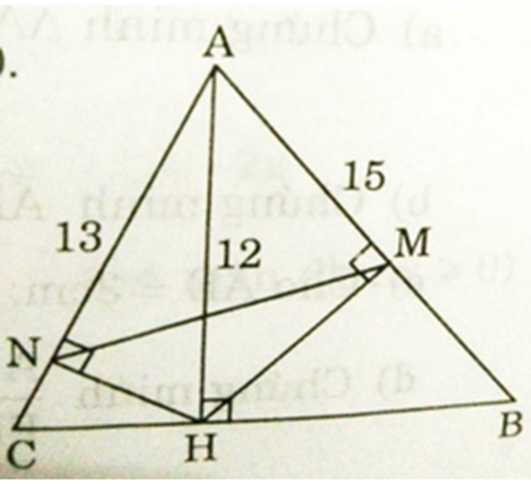
Cho tam giác ABC có ba góc nhọn, biết AB = 15cm, AC = 13cm và đường cao AH = 12cm. Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB. a) Chứng minh rằng ΔAHN ∼ ΔACH b) Tính độ dài BC c) Chứng minh ΔAMN ∼ ΔACB d) Tính MN (ảnh 1)

a) Xét ΔANH và ΔAHC có:

∠(NAH) chung

∠(ANH) = ∠(AHN) = 90^o

⇒ ΔANH ∼ ΔAHC (g.g)

b) Ta có :

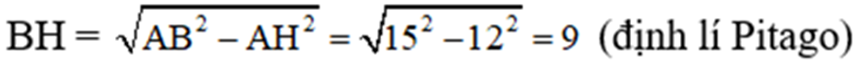
Cho tam giác ABC có ba góc nhọn, biết AB = 15cm, AC = 13cm và đường cao AH = 12cm. Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB. a) Chứng minh rằng ΔAHN ∼ ΔACH b) Tính độ dài BC c) Chứng minh ΔAMN ∼ ΔACB d) Tính MN (ảnh 2)

Tương tự : CH = 5 (cm)

⇒ BC = BH + CH = 9 + 5 = 14 (cm)

c) Theo chứng minh trên ta có:

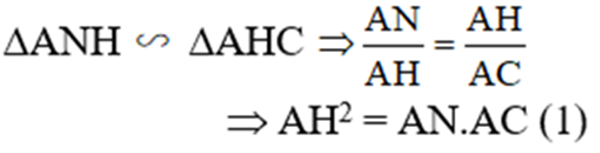
Cho tam giác ABC có ba góc nhọn, biết AB = 15cm, AC = 13cm và đường cao AH = 12cm. Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB. a) Chứng minh rằng ΔAHN ∼ ΔACH b) Tính độ dài BC c) Chứng minh ΔAMN ∼ ΔACB d) Tính MN (ảnh 3)

Chứng minh tương tự ta có :

ΔAMH ∼ ΔAHB ⇒ AH₂ = AM.AB (2)

Từ (1) và (2) ⇒ AN.AC = AM.AB (3)

Xét ΔAMN và ΔACB có :

∠A chung

AN.AC = AM.AB

⇒ ΔAMN ∼ ΔACB (c.g.c)

d) Ta có : ΔAMH ∼ ΔAHB

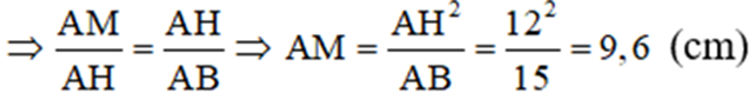
Lại có ΔAMN ∼ ΔACB (cmt)

Câu 2

Phương trình : x2 =-9 có nghiệm là :

A/ Một nghiệm x = 3

B/ Một nghiệm x = -3

C/ Có hai nghiệm : x = -3; x = 3

D/ Vô nghiệm

Lời giải

Đáp án D

Câu 3

Cho các đoạn thẳng AB=8cm ;CD = 6cm ; MN = 12mm. PQ = x. Tìm x để AB và CD tỉ lệ với MN;PQ

A/ x = 9 cm

B/ x = 0,9cm

C/ x = 18 cm

D/ Cả ba đều sai

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho ΔABC đồng dạng với ΔA’B’C’. Biết

và hiệu số chu vi của ΔA’B’C’và chu vi của ΔABC là 30. Phát biểu nào đúng

A/ C_ΔABC =20 ;C_{ΔA’B’C’}= 50

B/ C_{ΔABC =50} ;C_{ΔA’B’C’= 20}

C/ C_ΔABC = 45 ;C_{ΔA’B’C’}= 75

D/ Cả ba đều sai

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Phương trình :

có nghiệm là :

A/ 0

B/ 1

C/ 2

D/Kết quả khác

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

x ≥ 0 và x > 4 thì

A/ 0 ≤ x < 4

B/ x > 4

C/ x ≥ 4

D/ x ∈ ∅

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Hai người cùng làm chung một công việc hết 12 ngày. Năng suất trong một ngày của người thứ hai bằng 2/3 năng suất người thứ nhất. Hỏi nếu làm một mình thì mỗi người phải làm trong bao lâu mới xong công việc ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Vietjack official store

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

🔥 Đề thi HOT:

Bạn vui lòng để lại thông tin để được
TƯ VẤN THÊM

Hoặc gọi Hotline tư vấn: 084 283 45 85
Email: vietjackteam@gmail.com

VietJack