Quảng cáo
Trả lời:
b) Từ ý a),
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
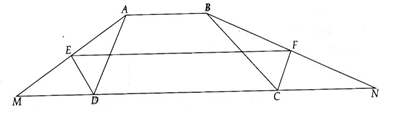
a) Gọi M và N lần lượt là giao điểm của AE, BF với CD.
Ta có: ngoài, ngoài.
Mà ngoài + ngoài = 1800 (do AB//CD)
, tức là tam giác ADE vuông tại E.
Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.
Chứng minh tương tự, ta được F là trung điểm của BN.
Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM
Lời giải
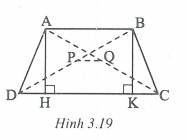
a) Vẽ ta được AH // BK và AB // HK
Ta có:
Theo ví dụ 4 thì đoạn thẳng PQ nối trung điểm của hai đường chéo bằng nửa hiệu hai đáy. Vậy HD = PQ
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.