Cho tam giác ABC vuông cân tại C, M là điểm bất kỳ trên cạnh AB . Vẽ tại E , tại F . Gọi D là trung điểm của AB . Chứng minh rằng:
a) Tứ giác CFME là hình chữ nhật.
Cho tam giác ABC vuông cân tại C, M là điểm bất kỳ trên cạnh AB . Vẽ tại E , tại F . Gọi D là trung điểm của AB . Chứng minh rằng:
a) Tứ giác CFME là hình chữ nhật.
Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 17: Ôn tập chương 1 có đáp án !!
Quảng cáo
Trả lời:
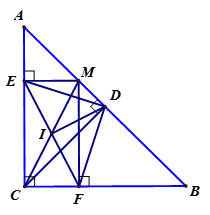
a) Theo giả thiết thì tứ giác CFME có 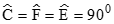
Do đó MECF là hình chữ nhật.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
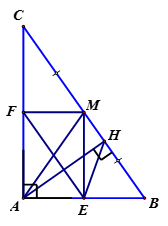
a) Theo tính chất tam giác vuông, ta có AM = MC = MB.
Tam giác CMA cân tại A và F là trung điểm AC suy ra .
Chứng minh tương tự: .
Vậy AEMF là hình chữ nhật.
Lời giải
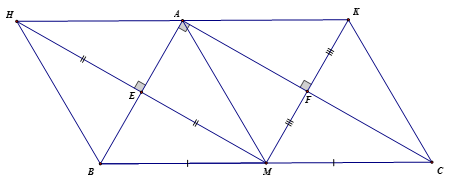
a) Xác định dạng của tứ giác
H là điểm đối xứng với M qua AB => AB là đường trung trực của HM
K là điểm đối xứng với M qua AC => AC là đường BM = CM = AM trung trực của KM
Lại có => AH = BH = BM = AM = MC = CK = AK
Tứ giác AEMF có nên tứ giác AEMF là hình chữ nhật
Tứ giác AMBH có AH = BH = BM = AM nên tứ giác AMBH là hình thoi
Tứ giác AMCK có AM = MC = CK = AK nên tứ giác AMCK là hình thoiLời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.