1. Lớp 8
  2. Toán
  3. Bài tập Toán 8 Chủ đề 17: Ôn tập chương 1 có đáp án

Dạng 2. Phiếu tự luyện số 2 có đáp án

24 người thi tuần này 4.6 2 K lượt thi 30 câu hỏi 45 phút

🔥 Đề thi HOT:

964 người thi tuần này

15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án

6 K lượt thi 15 câu hỏi
335 người thi tuần này

15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án

2.6 K lượt thi 15 câu hỏi
208 người thi tuần này

10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)

1 K lượt thi 10 câu hỏi
203 người thi tuần này

Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)

13.7 K lượt thi 18 câu hỏi
147 người thi tuần này

Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)

3.1 K lượt thi 21 câu hỏi
137 người thi tuần này

15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án

2 K lượt thi 15 câu hỏi
136 người thi tuần này

Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 10)

3.1 K lượt thi 15 câu hỏi
135 người thi tuần này

Dạng 4: Bài luyện tập 2 có đáp án

4.6 K lượt thi 13 câu hỏi

Nội dung liên quan:

Bài tập Toán 8 Chủ đề 1: Nhân đa, đơn thức có đáp án
lượt thi
1 đề

Bộ đề kiểm tra chuyên đề Toán 8 Chương 1 có đáp án
lượt thi
7 đề

Bài tập Toán 8 Chủ đề 1: Phân thức đại số có đáp án
lượt thi
7 đề

Bài tập Toán 8 Chủ đề 2: Tính chất cơ bản phân thức đại số có đáp án
lượt thi
5 đề

Bài tập Toán 8 Chủ đề 3: Rút gọn phân thức có đáp án
lượt thi
10 đề

Bài tập Toán 8 Chủ đề 4: Quy đồng mẫu thức nhiều phân thức có đáp án
lượt thi
3 đề

Bài tập Toán 8 Chủ đề 6: Phép cộng các phân thức đại số có đáp án
lượt thi
5 đề

Bài tập Toán 8 Chủ đề 7: Luyện tập phép cộng phân thức có đáp án
lượt thi
5 đề

Bài tập Toán 8 Chủ đề 8: Phép trừ các phân thức đại số có đáp án
lượt thi
9 đề

Bài tập Toán 8 Chủ đề 9: Luyện tập có đáp án
lượt thi
1 đề

Danh sách câu hỏi:

Câu 1

Cho tam giác ABC  vuông tại A , đường trung tuyến AM . Gọi H  là điểm đối xứng với M qua AB, E  là giao điểm của MH  và AB . Gọi K  là điểm đối xứng với M  qua AC , F  là giao điểm của MK  và AC .

a) Xác định dạng của tứ giác AEMF, AMBH, AMCK.

Lời giải

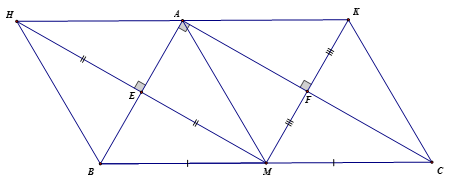
Cho tam giác ABC  vuông tại A , đường trung tuyến AM . a) Xác định dạng của tứ giác AEMF, AMBH, AMCK. (ảnh 1)

a) Xác định dạng của tứ giác AEMF, AMBH, AMCK

H là điểm đối xứng với M  qua AB => AB là đường trung trực của HM  

⇒AH=AM;BH=BM;AEM^=90°

K là điểm đối xứng với M  qua AC => AC là đường BM = CM = AM  trung trực của KM

 ⇒AM=AK;CM=CK;AFM^=90°

Lại có => AH = BH = BM = AM = MC = CK = AK

Tứ giác AEMF  có AEM^=AFM^=EAF^=90° nên tứ giác AEMF  là hình chữ nhật

Tứ giác AMBH  có AH = BH = BM = AM nên tứ giác AMBH là hình thoi

Tứ giác AMCK  có AM = MC = CK = AK  nên tứ giác AMCK  là hình thoi

Câu 2

b) Chứng minh rằng H đối xứng với K qua A .

Lời giải

b) Tứ giác AMBH, AMCK  là hình thoi => AH // BM; AK // MC mà M∈BC => A, H, K thẳng hàng (theo tiên đề Ơclit)

Lại có AH = AK  (cmt) A  là trung điểm của HK  hay H đối xứng với K  qua A

Câu 3

c) Tam giác vuông ABC có thêm điều kiện gì thì AEMF là hình vuông?

Lời giải

c) Hình chữ nhật AEMF  là hình vuông <=> EM = AE <=>AB = AC <=> △ABC  vuông cân tại A .

Câu 4

Cho tam giác nhọn ABC. Gọi H  là trực tâm của tam giác, M  là trung điểm của BC. Gọi D  là điểm đối xứng của H  qua M .

a. Chứng minh tứ giác BHCD  là hình bình hành.

Lời giải

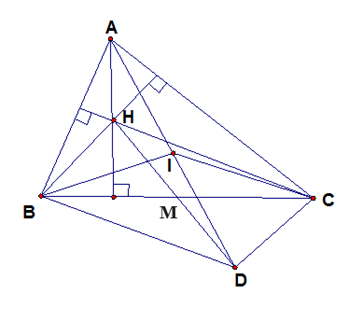
Cho tam giác nhọn ABC. Gọi H  là trực tâm của tam giác, M  là trung điểm của BC. Gọi D  là điểm đối xứng của H  qua M . a. Chứng minh tứ giác BHCD  là hình bình hành. (ảnh 1)

a. BHCD là hình bình hành:

 Vì M vừa là trung điểm của BC  vừa là trung điểm của HD  nên BHCD  là hình bình hành.

Câu 5

b. Chứng minh các tam giác ABD, ACD vuông tại B, C.

Lời giải

b. Tam giác ABD, ACD vuông tại B, C :

BD // CH mà CH ⊥AB⇒BD⊥AB  

CD // BH mà BH⊥AC⇒CD⊥AC

Câu 6

c. Gọi I là trung điểm của AD . Chứng minh rằng: IA = IB = IC = ID.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho tam giác ABC  vuông cân tại C, M là điểm bất kỳ trên cạnh AB . Vẽ ME⊥AC  tại E , MF ⊥BC  tại F . Gọi D là trung điểm của AB . Chứng minh rằng:

a) Tứ giác CFME  là hình chữ nhật.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

b) Tam giác DEF vuông cân.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Cho tam giác ABC  vuông tại A (AB < AC) , trung tuyến AM . E, F  lần lượt là trung điểm của AB, AC.

a) Chứng minh rằng AEMF  là hình chữ nhật.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

b) Gọi AH là đường cao của tam giác ABC. Chứng minh EHMF là hình thang cân

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Cho hình chữ nhật ABCD. Gọi M, N  lần lượt là trung điểm của BC, CD. Gọi giao điểm của AM, AN  với BD  lần lượt là P, Q . Gọi AC  cắt BD  tại O . Chứng minh rằng:

a) AP=23AM, AQ=23AN

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

b) BP = PQ = QD = 2OP.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Cho tứ giác ABCD  có ABCD . Gọi M, N, P, Q lần lượt là trung điểm của BC, BD, AD, AC. Chứng minh rằng:

a) Tứ giác MNPQ  là hình chữ nhật.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

b) Biết BC // AD, BC = 4cm, AD = 16cm. Tính MP

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Cho hình chữ nhật ABCD . Tia phân giác góc A^ cắt tia phân giác góc D^ tại M , tia phân giác góc B^ cắt tia phân giác góc C^  tại N . Gọi E, F  lần lượt là giao điểm của DM, CN  với AB. Chứng minh rằng:

a) AM = DM = BN = CN = ME = NF

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

b) Tứ giác DMNC là hình thang cân.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

c) AF = BE

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

c) AC, BD, MN  đồng quy

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Cho △ABC (A^=900) có AB < AC. Gọi M  là trung điểm của BC . Vẽ MD vuông góc với AB  tại D  và ME  vuông góc với AC  tại E . Vẽ đường cao AH  của △ABC .

a) Chứng minh ADME là hình chữ nhật.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

b) Chứng minh CMDE là hình bình hành.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

c) Chứng minh MHDE là hình thang cân.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

d) Qua A  kẻ đường thẳng song song với DH  cắt DE  tại K . Chứng minh HK⊥AC .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Cho hình bình hành ABCD  có AB  bằng đường chéo AC. Gọi O  là trung điểm của BC  và E  là điểm đối xứng của A  qua O. Đường thẳng vuông góc với AE  tại E  cắt AC  tại F .

a) Chứng minh ABEC  là hình thoi

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

b) Chứng minh tứ giác ADFE là hình chữ nhật

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

c) Vẽ CG⊥AB  tại G,CH⊥BE tại H . Chứng minh GH // AE .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

d) Vẽ AI⊥CD  tại I . Chứng minh rằng nếu AI = AO  thì AC⊥BD  và ABO^=60°

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Cho đoạn thẳng AG và điểm D nằm giữa hai điểm A và G. Trên cùng nửa mặt phẳng bờ AG  vẽ các hình vuông ABCD, DEFG. Gọi M, N lần lượt là trung điểm của AG, EC. Gọi I, K lần lượt là tâm đối xứng của các hình vuông ABCD, DEFG.

a) Chứng minh: AE = CG và AE⊥CG  tại H.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

b) Chứng minh IMKN là hình vuông.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

c) Chứng minh B, H , F thẳng hàng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

d) Gọi T  là giao điểm của BF  và EG . Chứng minh rằng độ dài TN  không đổi khi  di D động trên đoạn AG  cố định.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo

Đăng ký

Bạn đã có tài khoản?