d) Gọi T là giao điểm của BF và EG . Chứng minh rằng độ dài TN không đổi khi di D động trên đoạn AG cố định.
d) Gọi T là giao điểm của BF và EG . Chứng minh rằng độ dài TN không đổi khi di D động trên đoạn AG cố định.
Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 17: Ôn tập chương 1 có đáp án !!
Quảng cáo
Trả lời:
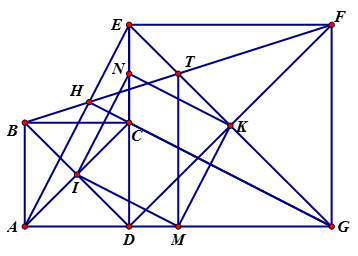
Ta có tứ giác ABCD, DEFG là hình vuông (gt) 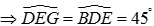
Mà hai góc này ở vị trí so le trong => EG // BD
Xét: BDF có K là trung điểm của DF mà EG // BD (cmt) hay TK // BD
=> T là trung điểm của BF
Ta có :
=> Tứ giác ABFG là hình thang
Ta có: T là trung điểm của BF (cmt), M là trung điểm của AG (gt)
=> TM là đường trung bình của hình thang ABFG
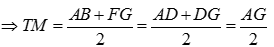
Mà AG không đổi nên độ dài TM không đổi khi D di động trên đoạn AG cố định.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
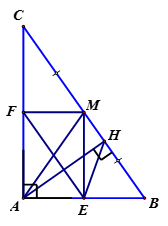
a) Theo tính chất tam giác vuông, ta có AM = MC = MB.
Tam giác CMA cân tại A và F là trung điểm AC suy ra .
Chứng minh tương tự: .
Vậy AEMF là hình chữ nhật.
Lời giải
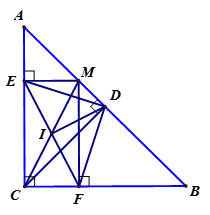
a) Theo giả thiết thì tứ giác CFME có 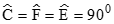
Do đó MECF là hình chữ nhật.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.