Thi Online Trắc nghiệm Toán 7 KNTT Bài 15: Các trường hợp bằng nhau của tam giác vuông có đáp án
Dạng 1: Tìm và chứng minh hai tam giác vuông bằng nhau có đáp án
-
293 lượt thi
-
10 câu hỏi
-
30 phút
Câu 1:
Cho hình vẽ sau, biết AB = AC:
Hãy chọn khẳng định sai.
Cho hình vẽ sau, biết AB = AC:
Hãy chọn khẳng định sai.
Đáp án đúng là: C
Ta xét từng đáp án:
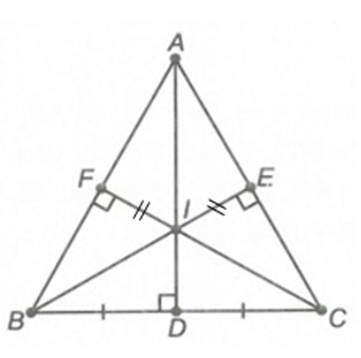
Đáp án A:
Xét ∆ADB và ∆ADC, có:
\[\widehat {ADB} = \widehat {ADC} = 90^\circ \] (AD ⊥ BC),
AD là cạnh chung,
BD = DC (giả thiết).
Do đó ∆ADB = ∆ADC (hai cạnh góc vuông).
Vậy A đúng.
Đáp án B:
Xét ∆IDB và ∆IDC, có:
\[\widehat {IDB} = \widehat {IDC} = 90^\circ \] (ID ⊥ BC),
ID là cạnh chung,
BD = DC (giả thiết).
Do đó ∆IDB = ∆IDC (hai cạnh góc vuông).
Vậy B đúng.
Đáp án C:
Xét ∆AFC và ∆AEB, có:
\[\widehat {AFC} = \widehat {AEB} = 90^\circ \],
\[\widehat A\] là góc chung,
AB = AC (giả thiết).
Do đó ∆AFC = ∆AEB (cạnh huyền – góc nhọn).
Do đó đáp án C sai vì chưa viết đúng thứ tự các đỉnh.
Thứ tự đúng là: ∆AFC = ∆AEB.
Đến đây ta có thể chọn đáp án C.
Đáp án D:
Xét ∆AFI và ∆AEI, có:
\[\widehat {AFI} = \widehat {AEI} = 90^\circ \],
AI là cạnh chung,
FI = EI (giả thiết).
Do đó ∆AFI = ∆AEI (cạnh huyền – cạnh góc vuông).
Vậy đáp án D đúng.
Vậy ta chọn đáp án C.
Câu 2:
Cho ∆ABC và ∆DEF có BC = EF, . Cần thêm điều kiện gì để ∆ABC = ∆DEF theo trường hợp cạnh huyền – cạnh góc vuông?
Cho ∆ABC và ∆DEF có BC = EF, . Cần thêm điều kiện gì để ∆ABC = ∆DEF theo trường hợp cạnh huyền – cạnh góc vuông?
Đáp án đúng là: C
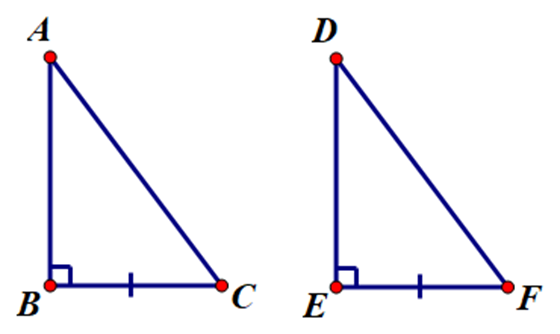
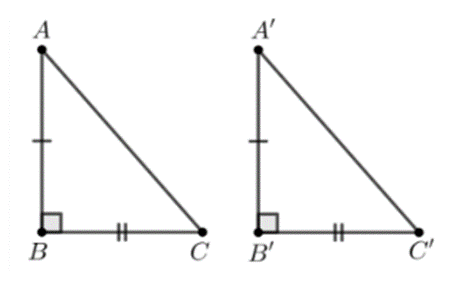
Vì ∆ABC vuông tại B nên BC là cạnh góc vuông.
Vì ∆DEF vuông tại E nên EF là cạnh góc vuông.
Do đó để ∆ABC = ∆DEF theo trường hợp cạnh huyền – cạnh góc vuông thì cần thêm điều kiện cạnh huyền của ∆ABC bằng cạnh huyền của ∆DEF (1).
Cạnh huyền của ∆ABC là: CA. (2)
Cạnh huyền của ∆DEF là: FD. (3)
Từ (1), (2) và (3) ta suy ra CA = FD.
Vậy ta chọn đáp án C.
Câu 3:
Cho ∆MNP và ∆GHI có \[\widehat M = \widehat G = 90^\circ \] và NP = HI. Cần thêm điều kiện gì để ∆MNP = ∆GHI theo trường hợp cạnh huyền – góc nhọn?
Cho ∆MNP và ∆GHI có \[\widehat M = \widehat G = 90^\circ \] và NP = HI. Cần thêm điều kiện gì để ∆MNP = ∆GHI theo trường hợp cạnh huyền – góc nhọn?
Đáp án đúng là: D
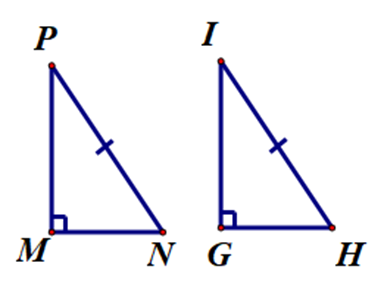
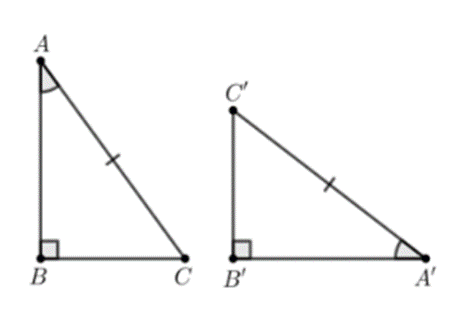
Bài toán cho sẵn: hai tam giác MNP và GHI có \[\widehat M = \widehat G = 90^\circ \] và NP = HI.
Ta thấy NP, HI lần lượt là cạnh huyền của ∆MNP và ∆GHI.
Do đó ta cần thêm điều kiện: góc nhọn của tam giác vuông này bằng góc nhọn tương ứng của tam giác vuông kia.
Ta thấy có thể xảy ra 2 trường hợp:
Trường hợp 1: \[\widehat N = \widehat H\].
Trường hợp 2: \[\widehat P = \widehat I\].
Do đó để ∆MNP = ∆GHI theo trường hợp cạnh huyền – góc nhọn, ta cần thêm điều kiện \[\widehat N = \widehat H\] hoặc \[\widehat P = \widehat I\].
Vậy ta chọn đáp án D.
Câu 4:
Cho ∆FDE và ∆PQR có: \[\widehat E = \widehat R = 90^\circ \], DF = QP, \[\widehat D = \widehat P = 30^\circ \]. Phát biểu nào sau đây đúng?
Cho ∆FDE và ∆PQR có: \[\widehat E = \widehat R = 90^\circ \], DF = QP, \[\widehat D = \widehat P = 30^\circ \]. Phát biểu nào sau đây đúng?
Đáp án đúng là: B
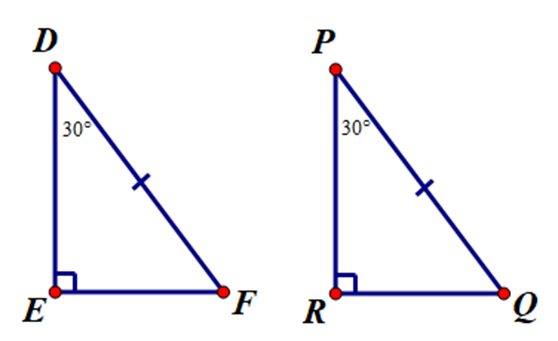
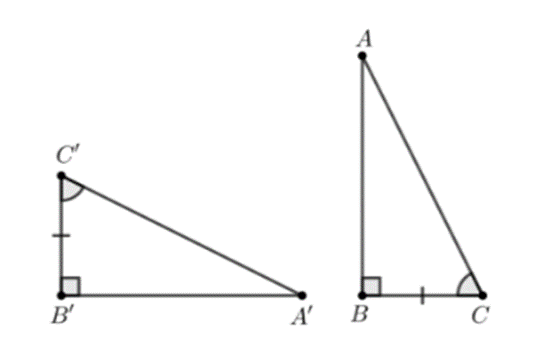
Xét ∆FDE và ∆QPR, có:
\[\widehat E = \widehat R = 90^\circ \].
DF = QP (giả thiết).
\[\widehat D = \widehat P = 30^\circ \].
Do đó ∆FDE = ∆QPR (cạnh huyền – góc nhọn).
Hay ta cũng có thể viết ∆DFE = ∆PQR;
Ta thấy đáp án A, C, D sai vì viết sai thứ tự các đỉnh.
Vậy ta chọn đáp án B.
Câu 5:
Cho hình vẽ sau:
Khẳng định nào sau đây là đúng?
Cho hình vẽ sau:
Khẳng định nào sau đây là đúng?
Đáp án đúng là: B
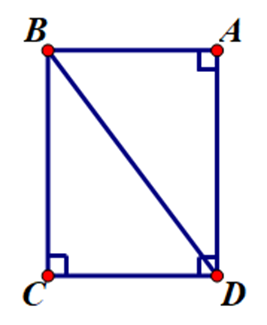
Tứ giác ABCD, có: \[\widehat A = \widehat C = \widehat D = 90^\circ \].
Do đó tứ giác ABCD là hình chữ nhật.
Ta suy ra AB = CD và AD = BC.
Xét ∆ABD và ∆CBD, có:
\[\widehat A = \widehat C = 90^\circ \].
AB = CD (chứng minh trên).
AD = CB (chứng minh trên).
Do đó ∆ABD = ∆CDB (hai cạnh góc vuông).
Các đáp án A, C, D sai vì viết sai thứ tự các đỉnh.
Vậy ta chọn đáp án B.
Bài thi liên quan
Có thể bạn quan tâm
Các bài thi hot trong chương
Đánh giá trung bình
0%
0%
0%
0%
0%