Câu hỏi:

21/08/2022 279

Cho tam giác nhọn ABC, các đường cao AA', BB', CC' cắt nhau tại H. Chứng minh rằng:

Xem lời giải

Câu hỏi trong đề: Trắc nghiệm chuyên đề Toán 8 Chủ đề 6. Ôn tập và kiểm tra có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

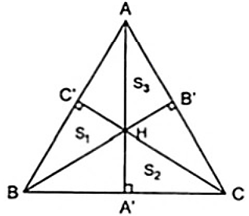
Cho tam giác nhọn ABC, các đường cao AA', BB', CC' cắt nhau tại H. Chứng minh rằng: (ảnh 2)

Gọi diện tích ABC, ABH,BCH,CAH lần lượt là S,S₁,S₂,S₃.

Ta có S = S₁ + S₂ + S₃.

+ Các tam giác ABC và ABH có chung đáy AB nên tỉ số đường cao bằng tỉ số diện tích: 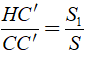Cho tam giác nhọn ABC, các đường cao AA', BB', CC' cắt nhau tại H. Chứng minh rằng: (ảnh 3)

+ Tương tự: 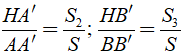Cho tam giác nhọn ABC, các đường cao AA', BB', CC' cắt nhau tại H. Chứng minh rằng: (ảnh 4)

Khi đó ta có 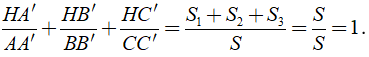Cho tam giác nhọn ABC, các đường cao AA', BB', CC' cắt nhau tại H. Chứng minh rằng: (ảnh 5)

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Đa giác đều là đa giác?

A. Có tất cả các cạnh bằng nhau.

B. Có tất cả các góc bằng nhau.

C. Có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

D. Cả 3 đáp án trên đều đúng

Lời giải

Chọn đáp án C.

Ta cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

Câu 2

Hai cạnh của một hình bình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp án ?

Xem đáp án

Lời giải

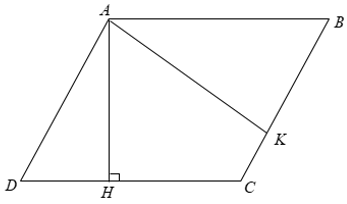
Hai cạnh của một hình bình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. (ảnh 1)

Xét hình bình bình ABCD có AB = CD = 8( cm ) và AD = BC = 6( cm )

Từ A kẻ các đường cao AH,AK.

Khi đó ta có:

+ S_hbh = AH.CD = 8.AH

+ S_hbh = AK.BC = 6.AK

Mà một hình bình hành thì chỉ có một diện tích chung nên 8.AH = 6.AK

Nếu độ dài đường cao thứ nhất là AH = 5( cm ) thì:

8.5 = 6.AK ⇔ AK = $\frac{8.5}{6}$ = $\frac{20}{3}$ ( cm ) là độ dài đường cao thứ hai.

Nếu độ dài đường cao thứ nhất là AK = 5( cm ) thì:

8.AH = 6.5 ⇔ AH = $\frac{6.5}{8}$ = $\frac{15}{4}$ ( cm ) là độ dài đường cao thứ hai.

Vậy bài toán này có hai đáp số

Câu 3

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?

A. Hình vuông là đa giác đều.

B. Tổng các góc của đa giác lồi 8 cạnh là 1080⁰.

C. Hình thoi là đa giác đều.

D. Số đo góc của hình bát giác đều là 135,5⁰.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Lục giác đều có?

A. Có 6 cạnh bằng nhau và 6 góc bằng nhau.

B. Có 6 cạnh bằng nhau và 6 góc bất kì

C. Có 5 cạnh bằng nhau và 5 góc bằng nhau.

D. Có 4 cạnh bằng nhau và 4 góc bằng nhau.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình thoi ABCD có chu vi bằng 40cm và đường chéo BD = 8cm. Diện tích của hình thoi là ?

A. 16( cm² )

B. 8√ 21 ( cm² )

C. 16√ 21 ( cm² )

D. 8( cm² )

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình thang vuông ABCD ( Aˆ = Dˆ = 90⁰ ), trong đó có Cˆ = 45⁰, AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là

A. 3( cm² )

B. 8( cm² )

C. 4( cm² )

D. 6( cm² )

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hình thoi có độ dài hai đường chéo lần lượt là 10cm, 12cm. Tính diện tích của hình thoi đó ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho tam giác nhọn ABC, các đường cao AA', BB', CC' cắt nhau tại H. Chứng minh rằng:

Bình luận

Đa giác đều là đa giác?

Hai cạnh của một hình bình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp án ?

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ? A. Hình vuông là đa giác đều. B. Tổng các góc của đa giác lồi 8 cạnh là 10800. C. Hình thoi là đa giác đều. D. Số đo góc của hình bát giác đều là 135,50.

Lục giác đều có?

Cho hình thoi ABCD có chu vi bằng 40cm và đường chéo BD = 8cm. Diện tích của hình thoi là ?

Cho hình thang vuông ABCD ( Aˆ = Dˆ = 900 ), trong đó có Cˆ = 450, AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là

Cho hình thoi có độ dài hai đường chéo lần lượt là 10cm, 12cm. Tính diện tích của hình thoi đó ?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?

A. Hình vuông là đa giác đều.

B. Tổng các góc của đa giác lồi 8 cạnh là 1080⁰.

C. Hình thoi là đa giác đều.

D. Số đo góc của hình bát giác đều là 135,5⁰.

Cho hình thang vuông ABCD ( Aˆ = Dˆ = 90⁰ ), trong đó có Cˆ = 45⁰, AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là