Câu hỏi:
12/07/2024 45,396
Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hình elip, chiều rộng của hầm là 12 m, khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m. Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao 2,8 m thì có chiều rộng không quá 3 m. Hỏi chiếc xe tải có chiều cao 2,8 m có thể đi qua hầm được không?
Câu hỏi trong đề: Giải SBT Toán 10 Bài 22. Ba đường conic có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Giả sử phương trình chính tắc của (E) là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (trong đó a > b > 0).
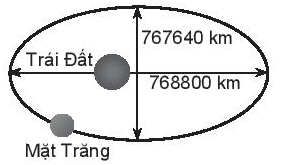
Vì chiều rộng của hầm là 12 m nên OA = 12 : 2 = 6 (m), do đó điểm A có tọa độ (6; 0).
Khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m nên OB = 3 m, do đó điểm B có tọa độ (0; 3).
Do các điểm B(0; 3) và A(6; 0) thuộc (E) nên thay vào phương trình của (E) ta có:
\(\frac{{{0^2}}}{{{a^2}}} + \frac{{{3^2}}}{{{b^2}}} = 1 \Rightarrow {b^2} = {3^2} = 9\)
\(\frac{{{6^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1 \Rightarrow {a^2} = {6^2} = 36\)
Suy ra phương trình của (E) là
\(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{9} = 1\).
Với những xe tải có chiều cao 2,8 m, chiều rộng của xe tải là 3 m, nếu xe chạy chính giữa hầm thì khoảng cách từ tâm xe tới mỗi bên xe khoảng 3 : 2 = 1,5 m, tương ứng với x = 1,5. Thay vào phương trình của elip để ta tìm ra độ cao y của điểm M (có hoành độ bằng 1,5 thuộc (E)) so với trục Ox.
\(\frac{{{x_M}^2}}{{36}} + \frac{{{y_M}^2}}{9} = 1\)
Suy ra: \({y_M} = 3.\sqrt {1 - \frac{{x_M^2}}{{36}}} = 3.\sqrt {1 - \frac{{{{1,5}^2}}}{{36}}} \approx 2,905 > 2,8\)
Kết luận: Ô tô tải có thể đi được qua hầm, tuy nhiên cần khuyến cáo ô tô phải đi vào chính giữa hầm.
Sách thầy cô Vietjack biên soạn
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
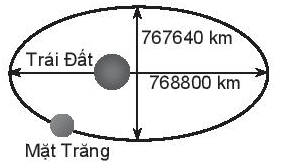
Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một đường elip với tâm Trái Đất là một tiêu điểm. Độ dài trục lớn, độ dài trục nhỏ của quỹ đạo lần lượt là 768 800 km và 767 640 km. Tìm khoảng cách lớn nhất và bé nhất từ tâm của Trái Đất đến Mặt Trăng.
Xem đáp án »
12/07/2024
21,101
Câu 2:
Viết phương trình chính tắc của hypebol (H), biết (H) đi qua điểm \(M\left( {3\sqrt 2 ; - 4} \right)\)và có một tiêu điểm là F2(5; 0).
Xem đáp án »
12/07/2024
20,651
Câu 3:
Cho elip (E) có phương trình \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{16}} = 1\). Tìm tiêu điểm và tiêu cự của elip.
Xem đáp án »
12/07/2024
7,702
Câu 4:
Viết phương trình chính tắc của parabol (P), biết rằng (P) có đường chuẩn là đường thẳng Δ: x + 4 = 0. Tìm toạ độ điểm M thuộc (P) sao cho khoảng cách từ M đến tiêu điểm của (P) bằng 5.
Xem đáp án »
12/07/2024
7,194
Câu 5:
Viết phương trình chính tắc của elip (E), biết (E) đi qua điểm A(6; 0) và có tiêu cự bằng 8.
Xem đáp án »
12/07/2024
6,687
Câu 6:
Cho hypebol (H) có phương trình\(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{{20}} = 1\). Tìm tiêu điểm và tiêu cự của hypebol.
Xem đáp án »
12/07/2024
6,037
🔥 Đề thi HOT:
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
-
15 câu Trắc nghiệm Toán 10 Kết nối tri thức Quy tắc đếm có đáp án
-
10 Bài tập Các bài toán thực tế ứng dụng nhị thức Newton (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận