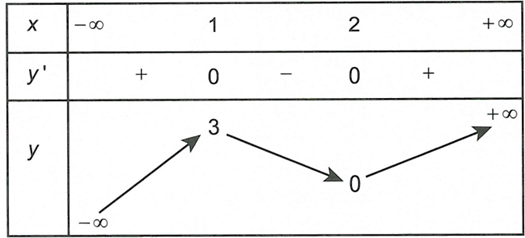
Cho hàm số có đồ thị (a, b là các số thực dương và ). Biết rằng (C) có tiệm cận ngang và có đúng một tiệm cận đứng.
Giá trị của tổng bằng
Cho hàm số có đồ thị (a, b là các số thực dương và ). Biết rằng (C) có tiệm cận ngang và có đúng một tiệm cận đứng.
Giá trị của tổng bằng
A. 8
B. 9
C. 6
D. 11
Câu hỏi trong đề: 194 câu Chuyên đề Toán 12 Bài 4: Tiệm cận có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Điều kiện
Phương trình tiệm cận ngang của đồ thị hàm số là
Đồ thị (C) có một tiệm cận đứng nên ta có các trường hợp sau:
Trường hợp 1: Phương trình có nghiệm kép và không là nghiệm của
. Vì nên
Thử lại ta có hàm số (thỏa mãn)
Vậy
Trường hợp 2: có hai nghiệm phân biệt và một trong hai nghiệm thỏa mãn . Điều này không xảy ra vì ab=4 .
Chọn D
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Phương trình các đường tiệm cận là .
Do đó hai đường tiệm cận và hai trục tọa độ tạo thành hình chữ nhật diện tích bằng 1.2 = 2 (đvdt).
Chọn D.
Câu 2
A. -5
B. 4
C. -1
D. 5
Lời giải
Hướng dẫn giải
Điều kiện .
Vì nên đồ thị luôn có một đường tiệm cận ngang với mọi m.
Ta có .
Xét . Để đồ thị hàm số có đúng hai đường tiệm cận thì phải nhận x=1 hoặc x=2 là nghiệm hay .
· Với , ta có hàm số nên đồ thị có hai đường tiệm cận là (thỏa mãn).
· Với , ta có hàm số nên đồ thị có hai đường tiệm cận là (thỏa mãn).
Vậy nên tổng các giá trị m bằng -5.
Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới.
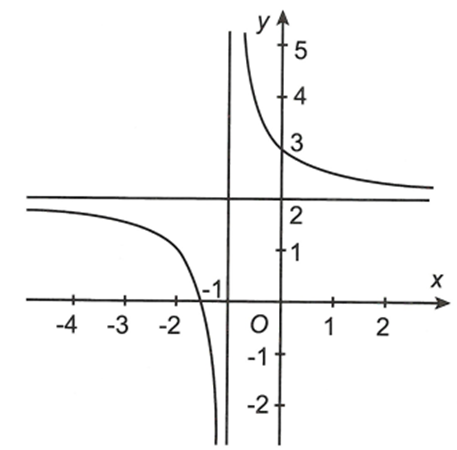
Phương trình các đường tiệm cận của đồ thị hàm số là
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới.

Phương trình các đường tiệm cận của đồ thị hàm số là
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.