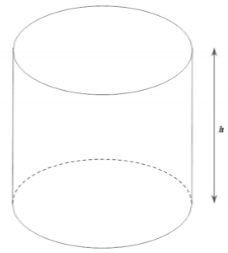
Muốn làm một bồn chứa 1000 lít hình trụ có nắp đậy. Hỏi chiều cao h (dm) của bồn gần với giá trị nào nhất để ít tốn vật liệu nhất?
A. 10, 5
B. 10,6
C. 10, 7
D. 10, 8
Quảng cáo
Trả lời:
Để ít tốn vật liệu nhất thì diện tích toàn phần bồn nước phải nhỏ nhất.
Tức là Stp= 2πR2+ 2πRh nhỏ nhất ( với R là bán kính đường tròn đáy)
Thể tích bồn nước V
Khi đó :
Sử dụng bảng biến thiên, ta tìm được Stp nhỏ nhất khi
Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
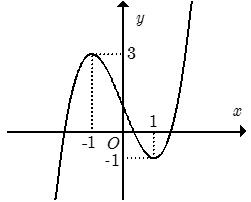
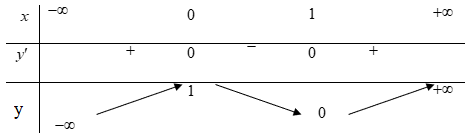
Câu 1
A. m=0
B. m= 2
C. m= 4
D. m= 5
Lời giải
+ Đạo hàm f'(x) = .
+ Suy ra hàm số f(x) là hàm số đơn điệu trên đoạn [1; 2] với mọi m≠ 1.
+ Khi đó ta có :
Chọn D.
Lời giải
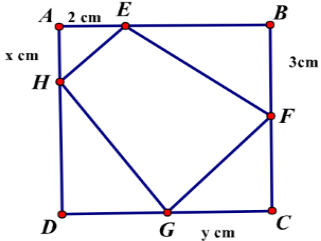
Ta có SEFGH nhỏ nhất lớn nhất
Tính được 2S= 2x+ 3y+ (6-x) (6-y) = xy-4x-3y+36 (1)
Mặt khác ∆ AEH đồng dạng ∆CGF nên
Từ (1) và (2) suy ra 2S =
Ta có 2S lớn nhất khi và chỉ khi nhỏ nhất.
Biểu thức nhỏ nhất nhỏ nhất
Vậy x+y =
Chọn D.
Câu 3
A. m= 1
B. m= -2
C. m= -1
D. m= -1 hoặc m= 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 2.
B. 0.
C. 6.
D. 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. -4
B. 2
C. 0
D . -2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. ½< m< 1
B. 0< m
C. m> 1
D. m< 1/2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Mai Ngọc
CHo nửa đường tròn tâm O đường kính AB =2R. Trên nửa đường lấy điểm C ( C khác A và B ). Gọi D là giao điểm của đường thẳg BC với tiếp tuyến tại A của nửa đường trong tâm O và I là trung điểm của AD
a. Chứng minh BC.BD = 4R^2
b. Chứng minh IC là tiếp tuyến của nửa đường tròn tâm O
c. Từ C kẻ CH vuông góc với AB ( H thuộc AB ) , BI cắt CH tại K. Chứng minh K là trung điểm của CH
Xem tất cả 1 phản hồi
trogiangvietjack
.
Mai Ngọc
CHo nửa đường tròn tâm O đường kính AB =2R. Trên nửa đường lấy điểm C ( C khác A và B ). Gọi D là giao điểm của đường thẳg BC với tiếp tuyến tại A của nửa đường trong tâm O và I là trung điểm của AD
a. Chứng minh BC.BD = 4R^2
b. Chứng minh IC là tiếp tuyến của nửa đường tròn tâm O
c. Từ C kẻ CH vuông góc với AB ( H thuộc AB ) , BI cắt CH tại K. Chứng minh K là trung điểm của CH
Xem tất cả 1 phản hồi
trogiangvietjack
.
Nhóc Dương'ss
Cho hàm số f(x) = a*x^2 +b*x + c tìm tất cả các giá trị thực của tham số m để phương trình f(x) +m -2018=0 có một nghiệm duy nhất
Xem tất cả 1 phản hồi
trogiangvietjack
.
Đang Ban
Thầy ởi
Đang Ban
Thầy ởi