10 Bài tập Xác định loại tam giác dựa vào số đo góc của tam giác đó (có lời giải)
64 người thi tuần này 4.6 696 lượt thi 10 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 03
Danh sách câu hỏi:
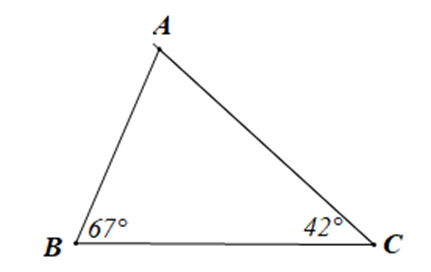
Câu 1
A. \(\widehat A = 71^\circ \) và tam giác ABC là tam giác nhọn;
B. \(\widehat A = 71^\circ \) và tam giác ABC là tam giác vuông;
C. \(\widehat A = 155^\circ \) tam giác ABC là tam giác đều;
D. \(\widehat A = 155^\circ \) tam giác ABC là tam giác tù.
Lời giải
Đáp án đúng là: A
Xét tam giác ABC có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat A = 180^\circ - \widehat B - \widehat C\)
Hay \(\widehat A = 180^\circ - 67^\circ - 42^\circ = 71^\circ \)
Ta thấy 42° < 67° < 71° < 90° nên góc A, góc B, góc C đều là góc nhọn.
Vậy \(\widehat A = 71^\circ \) và tam giác ABC là tam giác nhọn.
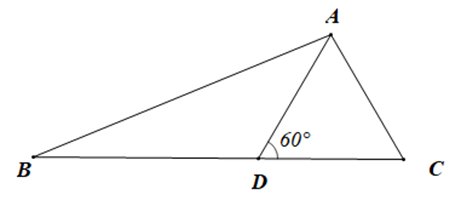
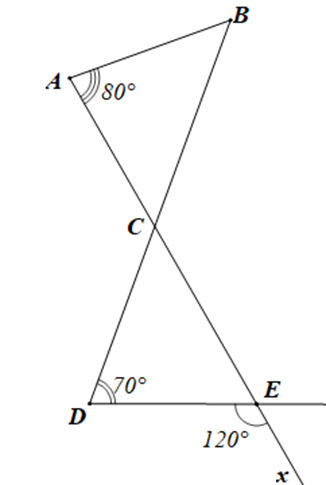
Câu 2
A. Tam giác nhọn;
B. Tam giác vuông;
C. Tam giác đều;
D. Tam giác tù.
Lời giải
Đáp án đúng là: D
Ta có \(\widehat {ADB}\) và \(\widehat {ADC}\) là hai góc kề bù nên \(\widehat {ADB} + \widehat {ADC} = 180^\circ \) (tính chất hai góc kề bù)
Suy ra \(\widehat {ADB} = 180^\circ - \widehat {ADC}\)
Hay \(\widehat {ADB} = 180^\circ - 60^\circ = 120^\circ > 90^\circ \)
Do đó góc ADB là góc tù
Vậy tam giác ABD là tam giác tù.
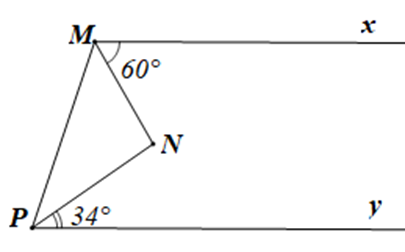
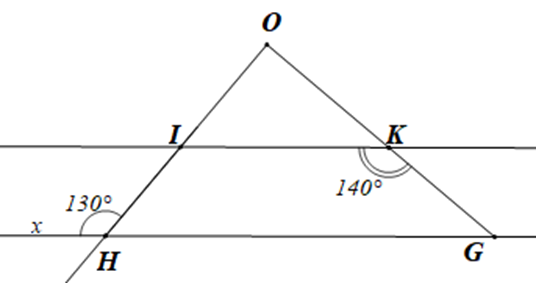
Câu 3
A. \(\widehat {MNP} = 86^\circ \) và tam giác MNP là tam giác nhọn;
B. \(\widehat {MNP} = 60^\circ \) và tam giác MNP là tam giác đều;
C. \(\widehat {MNP} = 90^\circ \) và tam giác MNP là tam giác vuông;
D. \(\widehat {MNP} = 94^\circ \) và tam giác MNP là tam giác tù.
Lời giải
Đáp án đúng là: D
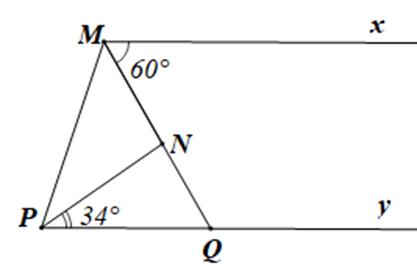
Kéo dài MN cắt Py tại Q.
Vì Mx // Py nên ta có: \(\widehat {xMQ} = \widehat {MQP}\) (hai góc so le trong)
Mà \(\widehat {xMQ} = 60^\circ \) do đó \(\widehat {MQP} = 60^\circ \)
Xét tam giác NPQ có \(\widehat {MNP}\) là góc ngoài của tam giác tại đỉnh N
Nên \(\widehat {MNP} = \widehat {NPQ} + \widehat {NQP}\) (tính chất góc ngoài của tam giác)
Suy ra \(\widehat {MNP} = 34^\circ + 60^\circ = 94^\circ > 90^\circ \)
Do đó góc MNP là góc tù
Vậy \(\widehat {MNP} = 94^\circ \) và tam giác MNP là tam giác tù.
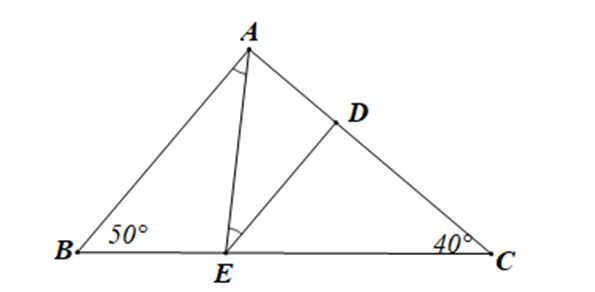
Câu 4
A. Tam giác nhọn;
B. Tam giác đều;
C. Tam giác vuông;
D. Tam giác tù.
Lời giải
Đáp án đúng là: C
Xét tam giác ABC có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat A = 180^\circ - \widehat B - \widehat C\)
Hay \(\widehat A = 180^\circ - 50^\circ - 40^\circ = 90^\circ \)
Xét hai đường thẳng DE và AB có: \(\widehat {BAE} = \widehat {AED}\)
Mà hai góc này ở vị trí so le trong
Do đó DE // AB
Suy ra \(\widehat {EDC} = \widehat A\) (hai góc ở vị trí đồng vị)
Mà \(\widehat A = 90^\circ \)
Do đó \(\widehat {EDC} = 90^\circ \)
Vậy tam giác CDE là tam giác vuông.
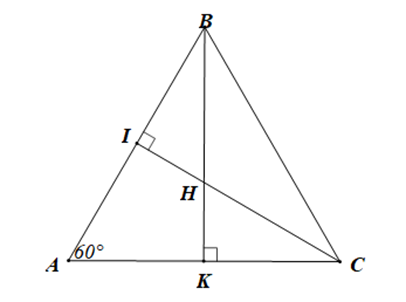
Câu 5
A. Tam giác tù;
B. Tam giác vuông;
C. Tam giác nhọn;
D. Tam giác đều.
Lời giải
Đáp án đúng là: A
Tam giác AIC vuông tại I \(\left( {\widehat I = 90^\circ } \right)\) nên \(\widehat A + \widehat {ACI} = 90^\circ \) (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \(\widehat A = 90^\circ - \widehat {ACI}\) (1)
Tam giác CHK vuông tại K \(\left( {\widehat K = 90^\circ } \right)\) nên \(\widehat {CHK} + \widehat {KCH} = 90^\circ \) (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \(\widehat {CHK} = 90^\circ - \widehat {KCH}\) (2)
Mà \(\widehat {ACI}\) chính là góc \(\widehat {KCH}\) (3)
Từ (1), (2) và (3) ta có: \(\widehat {CHK} = \widehat A = 60^\circ \)
Lại có \(\widehat {CHK}\) và \(\widehat {BHC}\) là hai góc kề bù nên \(\widehat {CHK} + \widehat {BHC} = 180^\circ \) (tính chất hai góc kề bù)
Suy ra \(\widehat {BHC} = 180^\circ - \widehat {CHK}\)
Do đó \(\widehat {BHC} = 180^\circ - 60^\circ = 120^\circ > 90^\circ \)
Khi đó góc BHC là góc tù
Vậy tam giác BHC là tam giác tù.
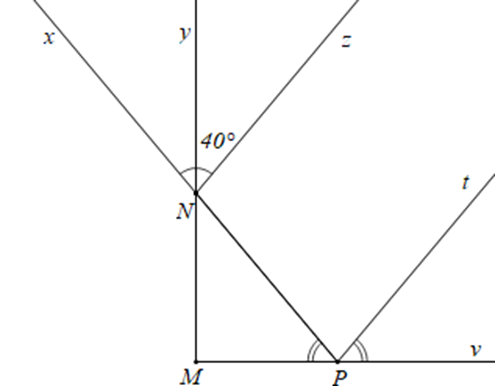
Câu 6
A. Tam giác tù;
B. Tam giác vuông;
C. Tam giác nhọn;
D. Tam giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Tam giác nhọn;
B. Tam giác đều;
C. Tam giác vuông;
D. Tam giác tù.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(\widehat {NPM} = 40^\circ \) và tam giác MNP và tam giác nhọn;
B. \(\widehat {NPM} = 50^\circ \) và tam giác MNP và tam giác nhọn;
C. \(\widehat {NPM} = 40^\circ \) và tam giác MNP và tam giác vuông;
D. \(\widehat {NPM} = 50^\circ \) và tam giác MNP và tam giác vuông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. Tam giác tù;
B. Tam giác vuông;
C. Tam giác nhọn;
D. Tam giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. Tam giác tù;
B. Tam giác nhọn;
C. Tam giác vuông;
D. Tam giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.