Câu hỏi:
12/07/2024 3,337
Trong một hoạt động ngoại khoá của trường, lớp Việt định mở một gian hàng bán bánh mì và nước khoáng. Biết rằng giá gốc một bánh mì là 15 000 đồng, một chai nước là 5 000 đồng. Các bạn dự kiến bán bánh mì với giá 20 000 đồng/1 bánh mì và nước giá 8 000 đồng/1 chai. Dựa vào thống kê số người tham gia hoạt động và nhu cầu thực tế các bạn dự kiến tổng số bánh mì và số chai nước không vượt qua 200. Theo quỹ lớp thì số tiền lớp Việt được dùng không quá 2 000 000 đồng. Hỏi lớp Việt có thể đạt được tối đa lợi nhuận là bao nhiêu ?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Gọi x, y lần lượt là số chiếc bánh mì và chai nước khoáng mà lớp Việt định mua để bán. Khi đó từ giả thiết ta có: x, y ∈ ℕ.
Mặt khác từ giả thiết ta có:
Dựa vào thống kê số người tham gia hoạt động và nhu cầu thực tế các bạn dự kiến tổng số bánh mì và số chai nước không vượt qua 200 nên:
x + y ≤ 200 (1)
Biết rằng giá gốc một bánh mì là 15 000 đồng, một chai nước là 5 000 đồng. Theo quỹ lớp thì số tiền lớp Việt được dùng không quá 2 000 000 đồng nên:
15 000x + 5 000y ≤ 2 000 000 (2)
Kết hợp (1) và (2) ta có hệ bất phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{x + y \le 200}\\{15\,\,000x + 5\,\,000y \le 2\,\,000\,\,000}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x + y \le 200}\\{3x + y \le 400}\end{array}} \right.\)
Tập nghiệm của hệ bất phương trình kết hợp với điều kiện x, y ∈ ℕ được biểu diễn bởi phần tô đậm trong hình vẽ dưới đây (tứ giác OABC)
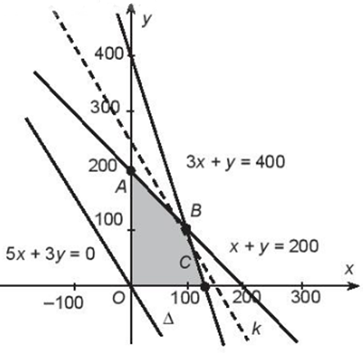
Nếu bán hết thì lợi nhuận lớp Việt có được là: d = 5x + 3y (nghìn đồng).
Để tìm lợi nhuận lớn nhất ta cần tìm giá trị lớn nhất của biểu thức:
d = 5x + 3y.
Khi đó các cặp (x; y) thoả mãn đề bài là các cặp số tự nhiên sao cho điểm M(x; y) nằm trong miền tứ giác OABC.
Ta có \(d:5x + 3y = \sqrt {34} .\frac{{\left| {5x + 3y} \right|}}{{\sqrt {{5^2} + {3^2}} }} = \sqrt {34} .d\left( {M,\Delta } \right)\)với Δ là đường thẳng có phương trình 5x + 3y = 0.
Gọi k là đường thẳng qua M và song song với Δ. Khi đó ta có d(M, Δ) = d(k, Δ). Do đó d lớn nhất tương ứng với khoảng cách giữa k và Δ lớn nhất. Từ hình vẽ ta có khoảng cách giữa k và Δ lớn nhất khi M trùng B. Do đó giá trị lớn nhất của d là
\(\sqrt {34} .\frac{{\left| {5.100 + 3.100} \right|}}{{\sqrt {{5^2} + {3^2}} }} = 800\)
Vậy lợi nhuận tối đa mà lớp Việt có thể đạt được là 800 nghìn đồng khi các bạn mua và bán được 100 chiếc bánh mì và 100 chai nước.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Do M thuộc Ox nên toạ độ của M có dạng M(m; 0).
Từ giả thiết ta có:
\(d\left( {M,\Delta } \right) = \frac{{\left| {3m + 0 - 3} \right|}}{{\sqrt {{3^2} + {1^2}} }} = \sqrt {10} \)
⇔ |3m – 3| = 10 (*)
TH1: 3m – 3 ≥ 0 hay m ≥ 1
Khi đó, ta có:
(*) ⇔ 3m – 3 = 10 ⇔ m = \(\frac{{13}}{3}\)(thỏa mãn)
TH2: 3m – 3 < 0 hay m < 1
Khi đó, ta có:
(*) ⇔ –3m + 3 = 10 ⇔ m = \( - \frac{7}{3}\) (thỏa mãn)
Vậy có hai điểm thoả mãn là \({M_1}\left( {\frac{{13}}{3};0} \right);{M_2}\left( { - \frac{7}{3};0} \right)\).
Lời giải
Hướng dẫn giải
Dựa vào phương trình đường thẳng d ta có:
x + y – 1 = 0
⇔ y = 1 – x
Do M thuộc đường thẳng d nên toạ độ của điểm M có dạng M(t; 1– t).
Chu vi tam giác ABM là: AB + MA + MB
Mà AB luôn không đổi nên chu vi tam giác ABM nhỏ nhất khi và chỉ khi MA + MB nhỏ nhất.
Lấy A’ đối xứng với A qua đường thẳng d. Khi đó ta có:
MA + MB = MA’ + MB ≥ A’B
Dấu bằng xảy ra khi M = A’B ∩ d
Gọi H là hình chiếu vuông góc của A lên d. Khi đó AH đi qua điểm A(–3;0) và nhận vectơ chỉ phương \(\overrightarrow {{u_d}} = \left( {1; - 1} \right)\) của đường thẳng d là vectơ pháp tuyến nên phương trình của AH là:
1(x + 3) – 1(y – 0) = 0
⇔ x – y + 3 = 0
Vậy toạ độ điểm H là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y - 1 = 0}\\{x - y + 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x + y = 1}\\{x - y = - 3}\end{array} \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 2\end{array} \right.} \right.\)
Suy ra H(–1; 2). Mặt khác, H là trung điểm của AA’ nên ta có:
xH = (xA + xA’) : 2 ⇔ xA’ = 2xH – xA = 2.(–1) – (–3) = 1
yH = (yA + yA’) : 2 ⇔ yA’ = 2yH – yA = 2.2 – 0 = 4
Do đó, ta có A’(1; 4)
Ta có \[\overrightarrow {A'B} = \left( {0; - 6} \right)\] là một vectơ chỉ phương của đường thẳng A’B. Do đó A’B là đường thẳng đi qua đểm A’(1; 4) và nhận \(\overrightarrow n = \left( {1;0} \right)\) là một vectơ pháp tuyến. Phương trình của đường thẳng A’B là:
1(x – 1) + 0(y – 4) = 0
⇔ x – 1 = 0
Vậy toạ độ điểm M là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y - 1 = 0}\\{x - 1 = 0}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}1 + y - 1 = 0\\x = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 0\end{array} \right.\)
Do đó ta có M(1; 0).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
15 câu Trắc nghiệm Toán 10 chân trời sáng tạo Không gian mẫu và biến cố có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận