Cho điểm M(x₀; y₀) thuộc elip (E) có phương trình \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{1} = 1\).

Tính MF₁² – MF₂²  theo x₀; y₀. Từ đó tính MF₁, MF₂, theo x₀; y₀.

Hướng dẫn giải

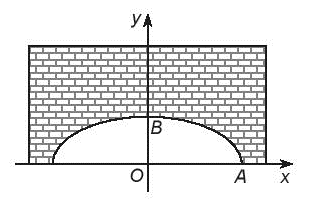
Giả sử phương trình chính tắc của (E) là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (trong đó a > b > 0).

Vì chiều rộng của hầm là 12 m nên OA = 12 : 2 = 6 (m), do đó điểm A có tọa độ (6; 0).

Khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m nên OB = 3 m, do đó điểm B có tọa độ (0; 3).

Do các điểm B(0; 3) và A(6; 0) thuộc (E) nên thay vào phương trình của (E) ta có:

\(\frac{{{0^2}}}{{{a^2}}} + \frac{{{3^2}}}{{{b^2}}} = 1 \Rightarrow {b^2} = {3^2} = 9\)

\(\frac{{{6^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1 \Rightarrow {a^2} = {6^2} = 36\)

Suy ra phương trình của (E) là

\(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{9} = 1\).

Với những xe tải có chiều cao 2,8 m, chiều rộng của xe tải là 3 m, nếu xe chạy chính giữa hầm thì khoảng cách từ tâm xe tới mỗi bên xe khoảng 3 : 2 = 1,5 m, tương ứng với x = 1,5. Thay vào phương trình của elip để ta tìm ra độ cao y của điểm M (có hoành độ bằng 1,5 thuộc (E)) so với trục Ox.

\(\frac{{{x_M}^2}}{{36}} + \frac{{{y_M}^2}}{9} = 1\)

Suy ra: \({y_M} = 3.\sqrt {1 - \frac{{x_M^2}}{{36}}} = 3.\sqrt {1 - \frac{{{{1,5}^2}}}{{36}}} \approx 2,905 > 2,8\)

Kết luận: Ô tô tải có thể đi được qua hầm, tuy nhiên cần khuyến cáo ô tô phải đi vào chính giữa hầm.

Hướng dẫn giải

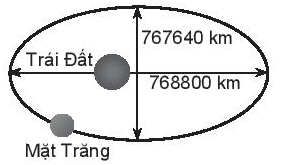
Xét đường elip như hình vẽ:

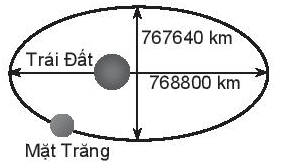
Theo đề bài: Độ dài trục lớn, độ dài trục nhỏ của quỹ đạo lần lượt là 768 800 km và 767 640 km. Nên ta có:

2a = 768 800 và 2b = 767 640

Do đó, a = 384 400 và b = 383 820.

Từ đó suy ra \[c = \sqrt {{a^2} - {b^2}} = \sqrt {{{384400}^2} - {{383820}^2}} \approx 21108\].

Vì vậy,

Khoảng cách lớn nhất từ tâm của Trái Đất đến Mặt Trăng là

a + c ≈ 384 400 + 21 108 = 405 508 (km)

Khoảng cách nhỏ nhất từ tâm của Trái Đất đến Mặt Trăng là:

a – c ≈ 384 400 – 21 108 = 363 292 (km).