Cho hình chữ nhật ABCD, đường chéo AC = d. Trên các cạnh AB, BC, CD và DA lần lượt lấy các điểm M, N, P, Q. Tính giá trị nhỏ nhất của tổng:
Cho hình chữ nhật ABCD, đường chéo AC = d. Trên các cạnh AB, BC, CD và DA lần lượt lấy các điểm M, N, P, Q. Tính giá trị nhỏ nhất của tổng:
Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 11: Hình chữ nhật có đáp án !!
Quảng cáo
Trả lời:
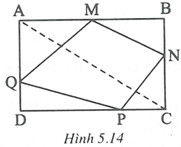
Tứ giác ABCD là hình chữ nhật nên
Áp dụng định lí Py-ta-go, ta có:
Do đó:
Vận dụng bất đẳng thức (dấu ''='' xảy ra khi a = b), ta được:
Vậy giá trị nhỏ nhất của tổng S là khi M, N, P, Q lần lượt là trung điểm của các cạnh hình chữ nhật.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
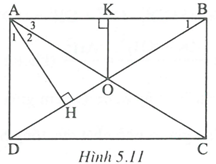
Gọi O là giao điểm của AC và BD, ta có OA = OC.
Vì nên AD = AO
Vẽ
Xét cân tại A, AH là đường cao => AH cũng là đường trung tuyến, cũng là đường phân giác.
Do đó và .
Vì nên .
(cạnh huyền, góc nhọn)
Xét vuông tại H có nên suy ra .
Hình bình hành ABCD có một góc vuông nên là hình chữ nhật.
Lời giải
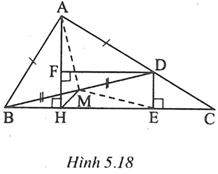
Vẽ
và có: ; AB = AD
(cùng phụ với ).
Do đó (cạnh huyền-góc nhọn)
=> AH = FD (1)
Tứ giác FDEH có ba góc vuông nên là hình chữ nhật
=> HE = FD (2)
Từ (1) và (2) suy ra: AH = HE
Ta có
Do đó tia HM là tia phân giác của góc AHC
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.