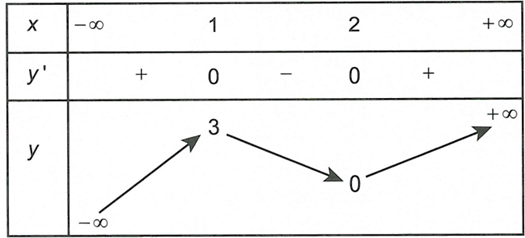
Cho hàm số bậc ba có đồ thị như hình vẽ.
![Cho hàm số bậc ba f(x)= ax^3+bx^2+cx+d có đồ thị như hình vẽ. Đồ thị hàm số g(x)= ( x^2-3x+2) căn x-1/ x [f^2(x)-f(x)] có bao nhiêu (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid5-1674808525.png)
Đồ thị hàm số có bao nhiêu đường tiệm cận đứng?
Cho hàm số bậc ba có đồ thị như hình vẽ.
![Cho hàm số bậc ba f(x)= ax^3+bx^2+cx+d có đồ thị như hình vẽ. Đồ thị hàm số g(x)= ( x^2-3x+2) căn x-1/ x [f^2(x)-f(x)] có bao nhiêu (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid5-1674808525.png)
Đồ thị hàm số có bao nhiêu đường tiệm cận đứng?
A. 4
B. 6
C. 3
D. 5
Câu hỏi trong đề: 194 câu Chuyên đề Toán 12 Bài 4: Tiệm cận có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Điều kiện xác định .
Xét phương trình .
Dựa vào đồ thị ta thấy
- Phương trình (1) có hai nghiệm phân biệt (loại) và (nghiệm kép).
- Phương trình (2) có ba nghiệm phân biệt , , .
Khi đó
Suy ra ,
trong đó , , nên đồ thị hàm số có ba tiệm cận đứng là x=2 ; ; .
Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Phương trình các đường tiệm cận là .
Do đó hai đường tiệm cận và hai trục tọa độ tạo thành hình chữ nhật diện tích bằng 1.2 = 2 (đvdt).
Chọn D.
Câu 2
A. -5
B. 4
C. -1
D. 5
Lời giải
Hướng dẫn giải
Điều kiện .
Vì nên đồ thị luôn có một đường tiệm cận ngang với mọi m.
Ta có .
Xét . Để đồ thị hàm số có đúng hai đường tiệm cận thì phải nhận x=1 hoặc x=2 là nghiệm hay .
· Với , ta có hàm số nên đồ thị có hai đường tiệm cận là (thỏa mãn).
· Với , ta có hàm số nên đồ thị có hai đường tiệm cận là (thỏa mãn).
Vậy nên tổng các giá trị m bằng -5.
Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới.
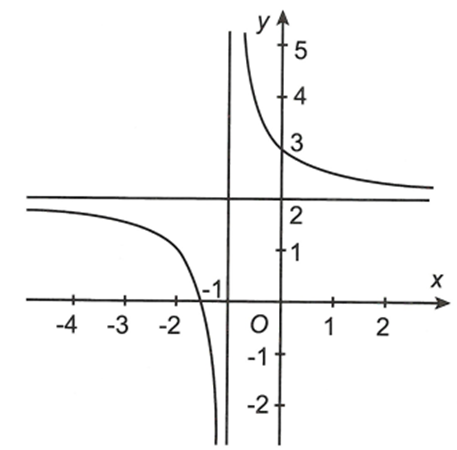
Phương trình các đường tiệm cận của đồ thị hàm số là
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới.

Phương trình các đường tiệm cận của đồ thị hàm số là
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.