Câu hỏi:
13/07/2022 390
Giả sử một người ăn kiêng cần được cung cấp ít nhất 300 calo, 36 đơn vị vitamin A và 90 đơn vị vitamin C mỗi ngày từ hai loại đồ uống I và II. Mỗi cốc đồ uống I cung cấp 60 calo, 12 đơn vị vitamin A và 10 đơn vị vitamin C.
Mỗi cốc đồ uống II cung cấp 60 calo, 6 đơn vị vitamin A và 30 đơn vị vitamin C. Biết rằng một cốc đồ uống I có giá 12 nghìn đồng và một cốc đồ uống II có giá 15 nghìn đồng.
Gọi F (nghìn đồng) là số tiền phải trả cho x cốc đồ uống I và y cốc đồ uống II. Hãy biểu diễn F theo x và y.
Giả sử một người ăn kiêng cần được cung cấp ít nhất 300 calo, 36 đơn vị vitamin A và 90 đơn vị vitamin C mỗi ngày từ hai loại đồ uống I và II. Mỗi cốc đồ uống I cung cấp 60 calo, 12 đơn vị vitamin A và 10 đơn vị vitamin C.
Mỗi cốc đồ uống II cung cấp 60 calo, 6 đơn vị vitamin A và 30 đơn vị vitamin C. Biết rằng một cốc đồ uống I có giá 12 nghìn đồng và một cốc đồ uống II có giá 15 nghìn đồng.
Gọi F (nghìn đồng) là số tiền phải trả cho x cốc đồ uống I và y cốc đồ uống II. Hãy biểu diễn F theo x và y.
Câu hỏi trong đề: Giải SBT Toán 10 Bài tập cuối chương 2 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
lời giải
Chi phí cho hai loại đồ uống là F(x; y) = 12x + 15y (nghìn đồng).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
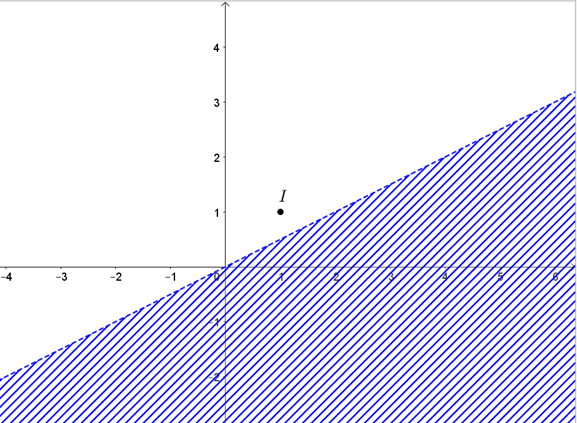
Biểu diễn tập nghiệm của bất phương trình -x + 2y > 0 trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: -x + 2y = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; 0) và (2; 1).
• Chọn điểm I(1; 1) d1 và thay vào biểu thức -x + 2y ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình -x + 2y > 0 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1) và bỏ đi đường thẳng d1.
Lời giải
Lời giải:
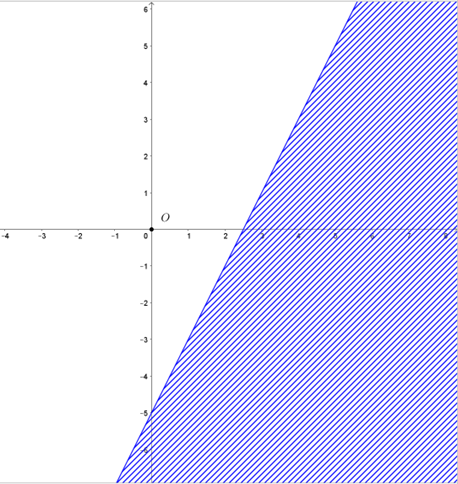
Biểu diễn tập nghiệm của bất phương trình 2x - y ≤ 5 trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: 2x - y = 5 bằng cách vẽ đường thẳng đi qua hai điểm (0; -5) và (3; 1).
• Chọn điểm O(0; 0) Ï d1 và thay vào biểu thức 2x - y ta được 0 < 5.
Suy ra miền nghiệm của bất phương trình 2x - y ≤ 5 là nửa mặt phẳng bờ d1 chứa điểm O(0; 0).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
làLời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
làLời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
làLời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
10 Bài tập Tìm hệ số, số hạng trong khai triển nhị thức Newton (có lời giải)
-
50 câu trắc nghiệm Thống kê cơ bản (phần 1)