Bộ 12 đề thi học kì 2 Toán 7 Cánh Diều cấu trúc mới có đáp án - Đề 08
18 người thi tuần này 5.0 6.3 K lượt thi 6 câu hỏi 45 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
6 câu Trắc nghiệm Toán 7 Bài 3: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh có đáp án (Vận dụng)
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
9 câu Trắc nghiệm Toán 7 Bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc có đáp án (Thông hiểu)
4 câu Trắc nghiệm Toán 7 Bài 5: Tính chất tia phân giác của một góc có đáp án (Thông hiểu)
10 câu Trắc nghiệm Toán 7 Bài 1: Tổng ba góc của một tam giác có đáp án (Thông hiểu)
5 câu Trắc nghiệm Tập hợp các số hữu tỉ có đáp án (Nhận biết)
5 câu Trắc nghiệm Toán 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu có đáp án (Nhận biết)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
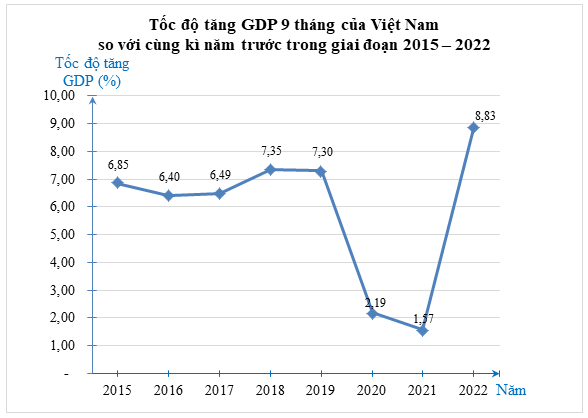
a) Bảng thống kê biểu diễn tốc độ tăng GDP 9 tháng của Việt Nam so với cùng kì năm trước trong giai đoạn 2015 – 2022 như sau:
|
Năm |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
2022 |
|
Tốc độ tăng 9 tháng so với cùng kì năm trước (%) |
\[6,85\] |
\[6,40\] |
\[6,49\] |
\[7,35\] |
\[7,30\] |
\[2,19\] |
\[1,57\] |
\[8,83\] |
b) Quan sát biểu đồ ta thấy tốc độ tăng GDP 9 tháng của Việt Nam so với cùng kì năm trước thấp nhất vào hai năm 2020 (với \[2,19\% \]) và 2021 (với \[1,57\% ).\]
Giải thích: Năm 2020 và năm 2021 bị ảnh hưởng bởi đại dịch COVID-19.
c) Tập hợp các kết quả xảy ra đối với năm được chọn là: \(A = \left\{ {2015;2016;...;2021;2022} \right\}\).
Tập hợp \(A\) có 8 phần tử.
Trong 8 năm (từ năm 2015 đến năm 2022) có 3 năm mà tốc độ tăng GDP 9 tháng của Việt Nam so với cùng kì năm trước cao hơn \(7\% \), đó là: năm 2018, năm 2019 và năm 2022 (lấy từ tập hợp \(A\)).
Xác suất để tốc độ tăng GDP 9 tháng của Việt Nam so với cùng kì năm trước cao hơn \(7\% \) là \(\frac{3}{8}\).
Lời giải
a) Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:
\(A = \left\{ {1;2;3;4;.....,;27;28} \right\}\).
Vậy có \(28\) phần tử
b) Kết quả thuận lợi của biến cố \(B\) là: \(5;10;15;20;25\).
Do đó, có 5 kết quả thuận lợi cho biến cố này.
Xác suất của biến cố trên là \(\frac{5}{{28}}.\)
c) Kết quả thuận lợi cho biến cố \(C\) là: \(11;21\). Do đó, có 2 kết quả thuận lợi cho biến cố này.
Xác suất của biến cố \(C\) là \(\frac{2}{{28}} = \frac{1}{{14}}.\)
Lời giải
a) Biểu thức biểu diễn số tiền mà bạn Dũng phải trả là: \(3x + 16y\) (đồng).
b) Ta có số tiền mà bạn Dũng phải trả nếu mua theo dự định là:
\(3.25{\rm{ }}000 + 16.9{\rm{ }}000 = 219{\rm{ }}000\) (đồng)
Do đó, số tiền mà bạn Dũng mang theo không đủ để mua bút và vở dự định.
Lời giải
a) \(A\left( x \right) = - \frac{5}{3}{x^2} + \frac{3}{4}{x^4} + 2x - \frac{7}{3}{x^2} - 3 + 4x + \frac{1}{4}{x^4}\)
\( = \left( {\frac{3}{4} + \frac{1}{4}} \right){x^4} + \left( { - \frac{5}{3} - \frac{7}{3}} \right){x^2} + \left( {2 + 4} \right)x - 3\)
\( = {x^4} - 4{x^2} + 6x - 3\).
b) Đa thức \(A\left( x \right)\) có bậc 4 và hệ số cao nhất là 1.
c) \(B\left( x \right) = \left( {{x^2} - 1} \right)\left( {{x^2} - 2} \right)\)
\( = {x^4} - 2{x^2} - {x^2} + 2\)
\( = {x^4} - 3{x^2} + 2\).
Ta có \(A\left( x \right) + C\left( x \right) = B\left( x \right)\)
Suy ra \(C\left( x \right) = B\left( x \right) - A\left( x \right)\)
\( = {x^4} - 3{x^2} + 2 - \left( {{x^4} - 4{x^2} + 6x - 3} \right)\)
\( = {x^4} - 3{x^2} + 2 - {x^4} + 4{x^2} - 6x + 3\)
\( = {x^2} - 6x + 5\).
d) Ta có:
• \(B\left( { - 1} \right) = {\left( { - 1} \right)^4} - 3.{\left( { - 1} \right)^2} + 2 = 1 - 3 + 2 = 0\).
Do đó \(x = - 1\) là nghiệm của đa thức \(B\left( x \right)\).
• \(C\left( { - 1} \right) = {\left( { - 1} \right)^2} - 6.\left( { - 1} \right) + 5 = 1 + 6 + 5 = 12\).
Do đó \(x = - 1\) không là nghiệm của đa thức \(C\left( x \right)\).
Lời giải
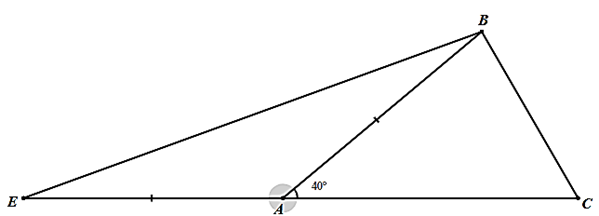
Xét \(\Delta ABC\) có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác) nên \(\widehat B + \widehat C = 140^\circ \).
Lại có \(\widehat B - \widehat C = 20^\circ \), do đó \(\widehat B = \frac{{140^\circ + 20^\circ }}{2} = 80^\circ \) và \(\widehat C = 60^\circ \).
Xét \(\Delta AEB\) cân tại \(A\) (do \(AE = AB\)) nên \(\widehat {AEB} = \widehat {ABE}\) (tính chất của tam giác cân) (1)
Lại có \(\widehat {BAC}\) là góc ngoài tam giác \(AEB\) nên \(\widehat {BAC} = \widehat {AEB} + \widehat {ABE}\) (2)
Từ (1) và (2) suy ra \(ABE = \frac{{\widehat {BAC}}}{2} = 20^\circ \).
Do đó, \(\widehat {CBE} = \widehat {CBA} + \widehat {ABE} = 80^\circ + 20^\circ = 100^\circ \).
5.2.
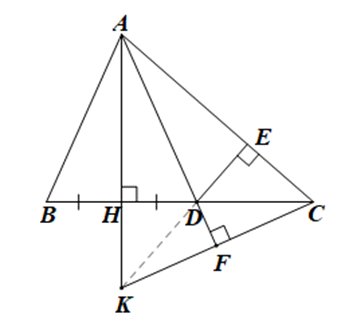
a) Xét \(\Delta ABC\) có \(AB < AC\) nên \(\widehat C < \widehat B\).
Mà \(\widehat C = 90^\circ - \widehat {HAC}\) và \(\widehat B = 90^\circ - \widehat {BAH}\).
Do đó \[90^\circ - \widehat {HAC} < 90^\circ - \widehat {BAH}\] hay \(\widehat {HAC} > \widehat {BAH}\).
b) Xét \(\Delta ABH\) và \(\Delta ADH\) có:
\(\widehat {AHB} = \widehat {AHD} = 90^\circ \);
\(AH\) là cạnh chung;
\(HB = HD\) (giả thiết).
Do đó \(\Delta ABH = \Delta ADH\) (hai cạnh góc vuông).
Suy ra \(AB = AD\) (hai cạnh tương ứng).
Tam giác \(ABD\) có \(AB = AD\) nên là tam giác cân tại \(A\).
c) Kéo dài \(AH\) và \(CF\) cắt nhau tại \(K\).
Xét \(\Delta AKC\) có \(CH \bot AK,AF \bot CK\), \(CH\) cắt \[AF\] tại \(D\) nên \(D\) là trực tâm của \(\Delta AKC\).
Suy ra \(KD \bot AC\)
Mà \(DE \bot AC\) nên ba điểm \(K,D,E\) thẳng hàng.
Vậy ba đường thẳng \(AH,DE,CF\) đồng quy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.